5.206. k_disjoint
| DESCRIPTION | LINKS | GRAPH |
- Origin
- Constraint
- Type
- Argument
- Restrictions
- Purpose
Given sets of domain variables, the constraint forces that no value is assigned to more than one set.
- Example
-
The constraint holds since:
The set of values and respectively assigned to the variables of the first and second collections have an empty intersection.
The set of values and respectively assigned to the variables of the first and third collections have an empty intersection.
The set of values and respectively assigned to the variables of the second and third collections have an empty intersection.
- Typical
- Symmetries
Items of are permutable.
Items of are permutable.
An occurrence of a value of can be replaced by any value of .
All occurrences of two distinct values of can be swapped; all occurrences of a value of can be renamed to any unused value.
- Arg. properties
Contractible wrt. .
- See also
- Keywords
characteristic of a constraint: disequality.
constraint type: system of constraints, decomposition, value constraint.
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
- Graph property(ies)
-
- Graph model
Parts (A) and (B) of Figure 5.206.1 respectively show the initial and final graph associated with the Example slot. To each vertex corresponds a collection of variables, while to each arc corresponds a constraint.
Figure 5.206.1. Initial and final graph of the constraint
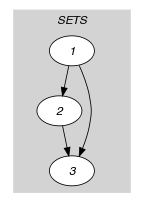
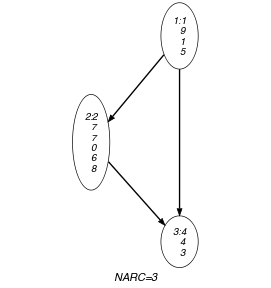
(a) (b)