5.394. symmetric
| DESCRIPTION | LINKS | GRAPH |
- Origin
- Constraint
- Argument
- Restrictions
- Purpose
Consider a digraph described by the collection. Select a subset of arcs of so that the corresponding graph is symmetric (i.e.,Β if there is an arc from to , there is also an arc from to ).
- Example
-
The constraint holds since the collection depicts a symmetric graph.
- Typical
- Symmetry
Items of are permutable.
- Algorithm
The filtering algorithm for the constraint is given inΒ [Dooms06]. It removes (respectively imposes) the arcs for which the arc is not present (respectively is present). It has an overall complexity of where and respectively denote the number of vertices and the number of arcs of the initial graph.
- See also
common keyword: Β (symmetric).
- Keywords
constraint arguments: constraint involving set variables.
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
- Graph class
-
- Graph model
PartΒ (A) of FigureΒ 5.394.1 shows the initial graph from which we start. It is derived from the set associated with each vertex. Each set describes the potential values of the attribute of a given vertex. PartΒ (B) of FigureΒ 5.394.1 gives the final graph associated with the Example slot.
Figure 5.394.1. Initial and final graph of the set constraint
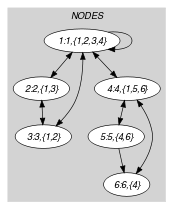
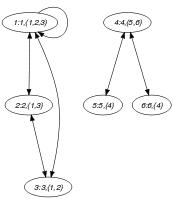
(a) (b)