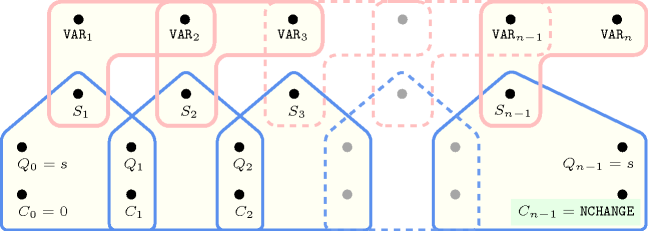
5.108. cyclic_change_joker
| DESCRIPTION | LINKS | GRAPH | AUTOMATON |
- Origin
- Constraint
- Arguments
- Restrictions
- Purpose
is the number of times that the following constraint holds:
and correspond to consecutive variables of the collection .
- Example
-
Since is set to and since is set to 4, a change between two consecutive items and of the collection corresponds to the fact that the condition holds. Consequently, the constraint holds since we have the two following changes (i.e., ) within :
A first change between 0 and 2,
A second change between 3 and 1.
But when the joker value 4 is involved, there is no change. This is why no change is counted between values 2 and 4, between 4 and 4 and between 1 and 4.
- Typical
- Symmetry
Items of can be shifted.
- Arg. properties
Functional dependency: determined by , and .
- Usage
The constraint can be used in the same context as the constraint with the additional feature: in our example codes 0 to 3 correspond to different type of activities (i.e., working the morning, the afternoon or the night) and code 4 represents a holiday. We want to express the fact that we do not count any change for two consecutive days , such that or is a holiday.
- See also
- Keywords
characteristic of a constraint: cyclic, joker value, automaton, automaton with counters.
constraint arguments: pure functional dependency.
constraint network structure: sliding cyclic(1) constraint network(2).
constraint type: timetabling constraint.
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
-
- Graph property(ies)
-
- Graph class
-
- Graph model
The joker values are those values that are greater than or equal to . We do not count any change for those arc constraints involving at least one variable taking a joker value.
Parts (A) and (B) of Figure 5.108.1 respectively show the initial and final graph associated with the Example slot. Since we use the graph property, the arcs of the final graph are stressed in bold.
Figure 5.108.1. Initial and final graph of the constraint
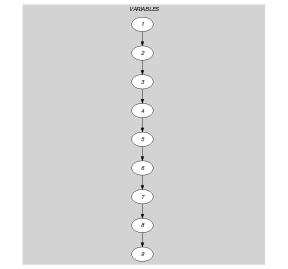
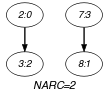
(a) (b)
- Automaton
Figure 5.108.2 depicts the automaton associated with the constraint. To each pair of consecutive variables of the collection corresponds a 0-1 signature variable . The following signature constraint links , and :
.
Figure 5.108.2. Automaton of the constraint
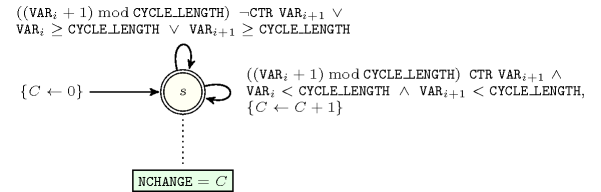
Figure 5.108.3. Hypergraph of the reformulation corresponding to the automaton of the constraint