5.311. orth_on_the_ground
| DESCRIPTION | LINKS | GRAPH |
- Origin
- Constraint
- Arguments
- Restrictions
- Purpose
The attribute of the item of the collection should be fixed to one.
- Example
-
The constraint holds since the attribute of its 1th item (i.e., 1th item since ) is set to one.
- Typical
- Used in
- Keywords
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
-
- Graph property(ies)
-
- Graph model
Parts (A) and (B) of Figure 5.311.1 respectively show the initial and final graph associated with the Example slot. Since we use the graph property, the loop of the final graph is stressed in bold.
Figure 5.311.1. Initial and final graph of the constraint
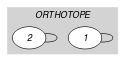
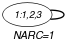
(a) (b) - Signature
Since all the attributes of the collection are distinct, because of the first condition of the arc constraint, and since we use the arc generator the final graph contains at most one arc. Therefore we can rewrite the graph property to and simplify to .