5.285. nset_of_consecutive_values
| DESCRIPTION | LINKS | GRAPH |
- Origin
N. Beldiceanu
- Constraint
- Arguments
- Restrictions
- Purpose
is the number of set of consecutive values used by the variables of the collection .
- Example
-
In the first example, the two parts and take respectively their values in the following sets of consecutive values and . Consequently, the corresponding constraint holds since its first argument is set to the number of sets of consecutive values.
- Typical
- Symmetries
Items of are permutable.
All occurrences of two distinct values of can be swapped.
One and the same constant can be added to the attribute of all items of .
- Arg. properties
Functional dependency: determined by .
- Usage
Used for specifying the fact that the values have to be used in a compact way is achieved by setting to 1.
- Counting
-
Length () 2 3 4 5 6 7 8 Solutions 9 64 625 7776 117649 2097152 43046721 Number of solutions for : domains
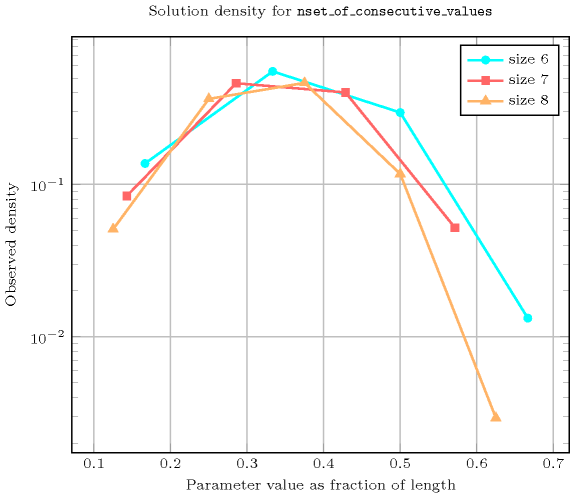
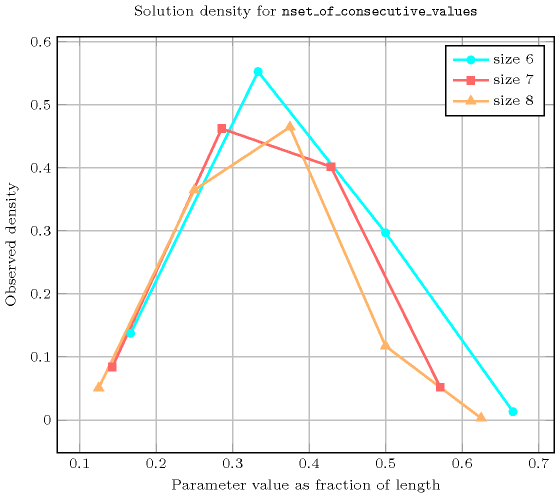
Length () 2 3 4 5 6 7 8 Total 9 64 625 7776 117649 2097152 43046721 Parameter value 1 7 34 217 1716 16159 176366 2187637 2 2 30 372 4740 65010 969066 15695624 3 - - 36 1320 34920 842520 19989900 4 - - - - 1560 109200 5047560 5 - - - - - - 126000 Solution count for : domains
- See also
- Keywords
characteristic of a constraint: consecutive values.
constraint arguments: pure functional dependency.
constraint type: value constraint.
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
- Graph property(ies)
-
- Graph model
Since the arc constraint is symmetric each strongly connected component of the final graph corresponds exactly to one connected component of the final graph.
Parts (A) and (B) of Figure 5.285.1 respectively show the initial and final graph associated with the first example of the Example slot. Since we use the graph property, we show the two strongly connected components of the final graph.
Figure 5.285.1. Initial and final graph of the constraint
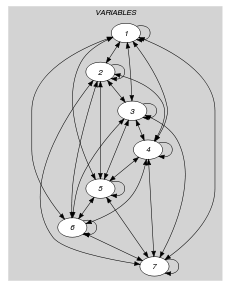
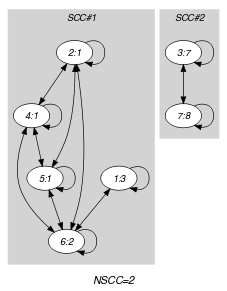
(a) (b)