5.157. full_group
| DESCRIPTION | LINKS | AUTOMATON |
- Origin
- Constraint
- Synonym
.
- Arguments
- Restrictions
- Purpose
Let be the number of variables of the collection . Let be consecutive variables of the collection of variables such that all the following conditions simultaneously apply:
All variables take their value in the set of values ,
or does not take a value in ,
or does not take a value in .
We call such a sequence of variables a group. A full group is a group that neither starts at position 1 nor ends at position . Similarly an anti-full group is a maximum sequence of variables that are not assigned any value from that neither starts at position 1 nor ends at position .
The constraint is true if all the following conditions hold:
There are exactly full groups of variables,
is the number of variables of the smallest full group,
is the number of variables of the largest full group,
is the number of variables of the smallest anti-full group,
is the number of variables of the largest anti-full group,
is the number of variables that belong to a full group.
- Example
-
Given the fact that full groups are formed by even values in (i.e., values expressed by the collection), the constraint holds since:
Its first argument, , is set to value 2 since the sequence contains two full groups of even values (i.e., group and group ). Note that the first 0 is not a full group since it is located at the first position of the sequence.
Its second argument, , is set to value 2 since the smallest full group of even values involves only two elements (i.e., the full group ).
Its third argument, , is set to value 3 since the largest full group of even values involves three elements (i.e., the full group ).
Its fourth argument, , is set to value 1 since the smallest anti-full groups involve a single element (i.e., the anti-full groups 1 and 7).
Its fifth argument, , is set to value 1 since the largest anti-full groups involve a single element (i.e., the anti-full groups 1 and 7).
Its sixth argument, , is set to value 5 since the total number of even values part of a full group of the sequence is equal to 5 (i.e., elements 2, 6, 2, 4 and 8).
- Typical
- Symmetries
Items of can be reversed.
Items of are permutable.
An occurrence of a value of that belongs to (resp. does not belong to ) can be replaced by any other value in (resp. not in ).
- Arg. properties
Functional dependency: determined by and .
Functional dependency: determined by and .
Functional dependency: determined by and .
Functional dependency: determined by and .
Functional dependency: determined by and .
Functional dependency: determined by and .
- See also
- Keywords
characteristic of a constraint: automaton, automaton with counters, automaton with same input symbol.
combinatorial object: sequence.
constraint arguments: reverse of a constraint, pure functional dependency.
constraint network structure: alpha-acyclic constraint network(2), alpha-acyclic constraint network(3).
- Automaton
Figures 5.157.1, 5.157.3, 5.157.5, 5.157.7, 5.157.9 and 5.157.11 depict the different automata associated with the constraint. For the automata that respectively compute , , , , and we have a 0-1 signature variable for each variable of the collection . The following signature constraint links and : .
Figure 5.157.1. Automaton for the argument of the constraint and its glue matrix
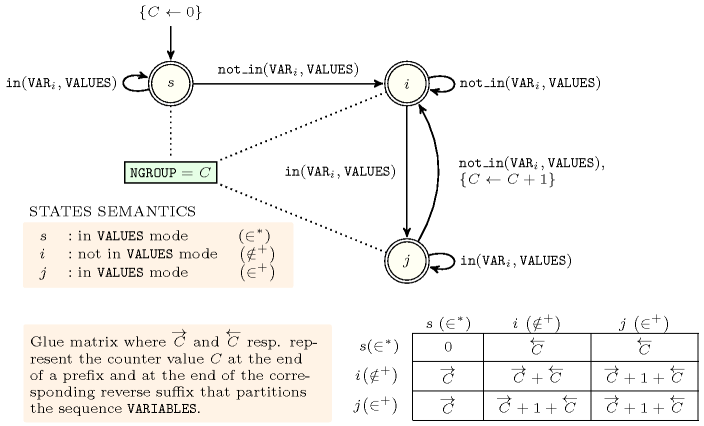
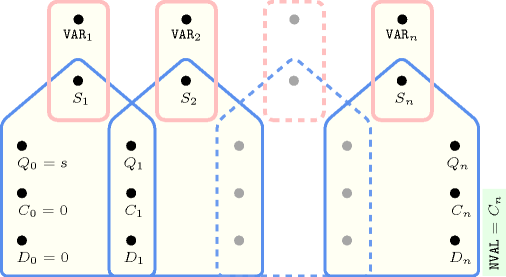
Figure 5.157.2. Hypergraph of the reformulation corresponding to the automaton (with one counter) of the argument of the constraint (since all states of the automaton are accepting there is no restriction on the last variable )
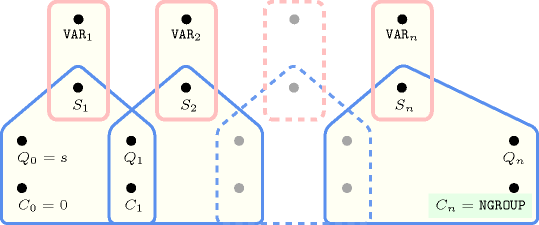
Figure 5.157.3. Automaton for the argument of the constraint
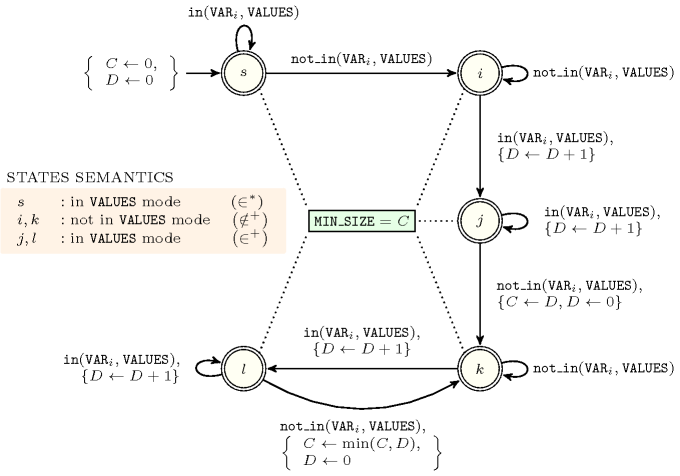
Figure 5.157.4. Hypergraph of the reformulation corresponding to the automaton (with two counters) of the argument of the constraint (since all states of the automaton are accepting there is no restriction on the last variable )
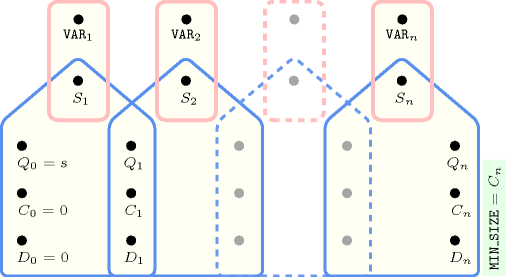
Figure 5.157.5. Automaton for the argument of the constraint and its glue matrix
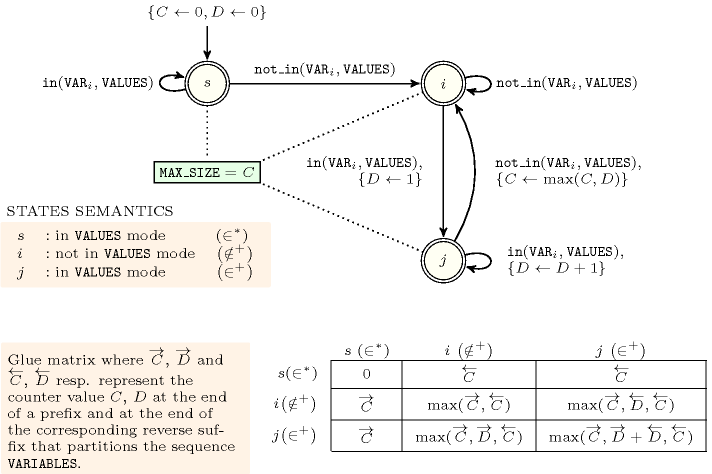
Figure 5.157.6. Hypergraph of the reformulation corresponding to the automaton (with two counters) of the argument of the constraint (since all states of the automaton are accepting there is no restriction on the last variable )
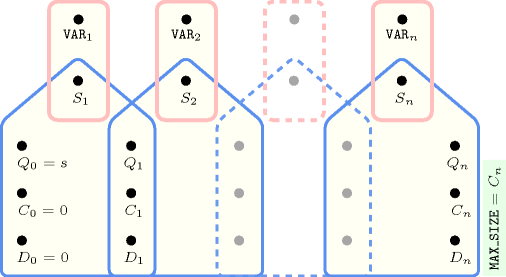
Figure 5.157.7. Automaton for the argument of the constraint
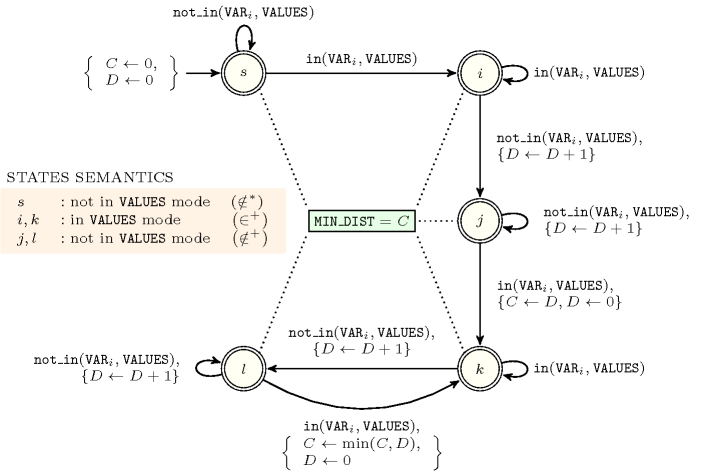
Figure 5.157.8. Hypergraph of the reformulation corresponding to the automaton (with two counters) of the argument of the constraint (since all states of the automaton are accepting there is no restriction on the last variable )
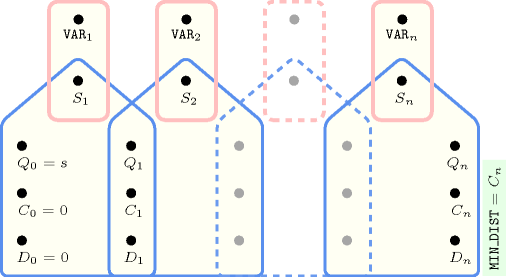
Figure 5.157.9. Automaton for the argument of the constraint and its glue matrix
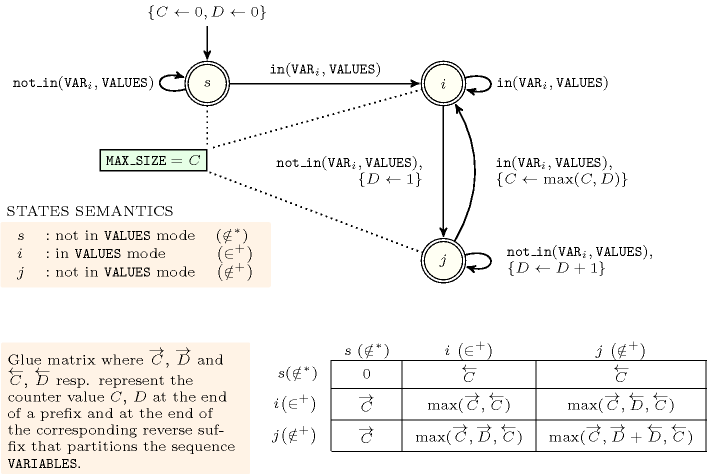
Figure 5.157.10. Hypergraph of the reformulation corresponding to the automaton (with two counters) of the argument of the constraint (since all states of the automaton are accepting there is no restriction on the last variable )
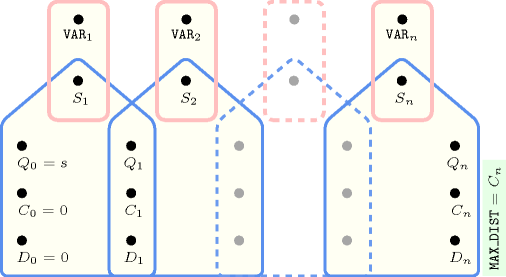
Figure 5.157.11. Automaton for the argument of the constraint and its glue matrix
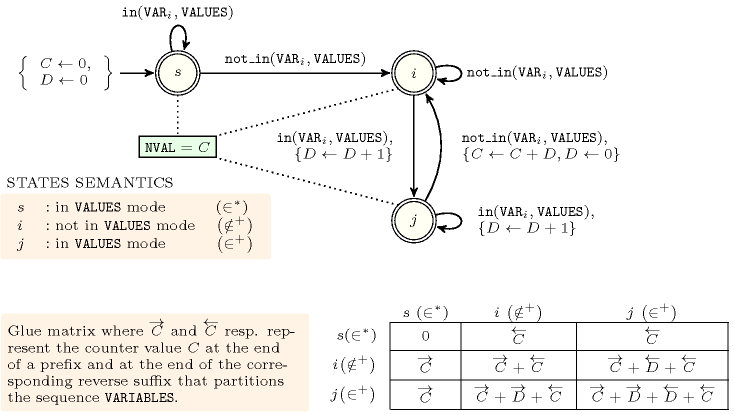
Figure 5.157.12. Hypergraph of the reformulation corresponding to the automaton (with two counters) of the argument of the constraint (since all states of the automaton are accepting there is no restriction on the last variable )