5.140. element_greatereq
| DESCRIPTION | LINKS | GRAPH | AUTOMATON |
- Origin
- Constraint
- Arguments
- Restrictions
- Purpose
is greater than or equal to one of the entries (i.e., the attribute) of the table .
- Example
-
The constraint holds since is greater than or equal to .
- Typical
- Symmetries
Items of are permutable.
All occurrences of two distinct values in or can be swapped; all occurrences of a value in or can be renamed to any unused value.
- Usage
Used for modelling variable subscripts in linear constraints [OttossonThorsteinssonHooker99].
- Reformulation
By introducing an extra variable , the constraint can be expressed in term of an constraint and of an inequality constraint .
- See also
common keyword: , , (array constraint).
- Keywords
characteristic of a constraint: automaton, automaton without counters, reified automaton constraint.
constraint arguments: binary constraint.
constraint network structure: centered cyclic(2) constraint network(1).
constraint type: data constraint.
filtering: linear programming, arc-consistency.
modelling: array constraint, table, variable subscript, variable indexing.
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
-
- Graph property(ies)
-
- Graph model
Similar to the constraint except that the equality constraint of the second condition of the arc constraint is replaced by a greater than or equal to constraint.
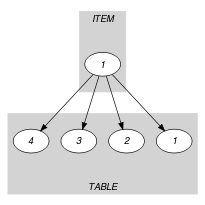
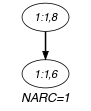
Parts (A) and (B) of Figure 5.140.1 respectively show the initial and final graph associated with the Example slot. Since we use the graph property, the unique arc of the final graph is stressed in bold.
Figure 5.140.1. Initial and final graph of the constraint
(a) (b) - Signature
Since all the attributes of are distinct and because of the first arc constraint the final graph cannot have more than one arc. Therefore we can rewrite to and simplify to .
- Automaton
Figure 5.140.2 depicts the automaton associated with the constraint. Let and respectively be the and the attributes of the unique item of the collection. Let and respectively be the and the attributes of the item of the collection. To each quadruple corresponds a 0-1 signature variable as well as the following signature constraint: .
Figure 5.140.2. Automaton of the constraint
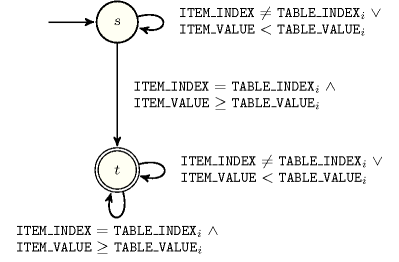
Figure 5.140.3. Hypergraph of the reformulation corresponding to the automaton of the constraint