Global Constraint Catalog: Crelaxed_sliding

5.331. relaxed_sliding_sum

DESCRIPTION

LINKS

GRAPH

Origin

CHIP

Constraint

$𝚛𝚎𝚕𝚊𝚡𝚎𝚍_𝚜𝚕𝚒𝚍𝚒𝚗𝚐_𝚜𝚞𝚖 (𝙰𝚃𝙻𝙴𝙰𝚂𝚃, 𝙰𝚃𝙼𝙾𝚂𝚃, 𝙻𝙾𝚆, 𝚄𝙿, 𝚂𝙴𝚀, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

Arguments

$𝙰𝚃𝙻𝙴𝙰𝚂𝚃$	$𝚒𝚗𝚝$
$𝙰𝚃𝙼𝙾𝚂𝚃$	$𝚒𝚗𝚝$
$𝙻𝙾𝚆$	$𝚒𝚗𝚝$
$𝚄𝙿$	$𝚒𝚗𝚝$
$𝚂𝙴𝚀$	$𝚒𝚗𝚝$
$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)$

Restrictions

𝙰𝚃𝙻𝙴𝙰𝚂𝚃 \geq 0

𝙰𝚃𝙼𝙾𝚂𝚃 \geq 𝙰𝚃𝙻𝙴𝙰𝚂𝚃

𝙰𝚃𝙼𝙾𝚂𝚃 \leq | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | - 𝚂𝙴𝚀 + 1

𝚄𝙿 \geq 𝙻𝙾𝚆

𝚂𝙴𝚀 > 0

𝚂𝙴𝚀 \leq | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚟𝚊𝚛)

Purpose

There are between $𝙰𝚃𝙻𝙴𝙰𝚂𝚃$ and $𝙰𝚃𝙼𝙾𝚂𝚃$ sequences of $𝚂𝙴𝚀$ consecutive variables of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ such that the sum of the variables of the sequence is in $[𝙻𝙾𝚆, 𝚄𝙿]$ .

Example

(3, 4, 3, 7, 4, 〈2, 4, 2, 0, 0, 3, 4〉)

Within the sequence $2420034$ we have exactly 3 subsequences of $𝚂𝙴𝚀 = 4$ consecutive values such that their sum is located within the interval $[𝙻𝙾𝚆, 𝚄𝙿] = [3, 7]$ : subsequences $4200$ , $2003$ and $0034$ . Consequently the $𝚛𝚎𝚕𝚊𝚡𝚎𝚍_𝚜𝚕𝚒𝚍𝚒𝚗𝚐_𝚜𝚞𝚖$ constraint holds since the number of such subsequences is located within the interval $[𝙰𝚃𝙻𝙴𝙰𝚂𝚃, 𝙰𝚃𝙼𝙾𝚂𝚃] = [3, 4]$ .

Typical

𝚂𝙴𝚀 > 1

𝚂𝙴𝚀 < | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |

𝚛𝚊𝚗𝚐𝚎

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) > 1

𝙰𝚃𝙻𝙴𝙰𝚂𝚃 > 0 \lor 𝙰𝚃𝙼𝙾𝚂𝚃 < | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | - 𝚂𝙴𝚀 + 1

Symmetries

$𝙰𝚃𝙻𝙴𝙰𝚂𝚃$ can be decreased to any value $\geq 0$ .
$𝙰𝚃𝙼𝙾𝚂𝚃$ can be increased to any value $\leq | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | - 𝚂𝙴𝚀 + 1$ .
Items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ can be reversed.

Algorithm

[BeldiceanuCarlsson01].

See also

hard version: $𝚜𝚕𝚒𝚍𝚒𝚗𝚐_𝚜𝚞𝚖$ .

used in graph description: $𝚜𝚞𝚖_𝚌𝚝𝚛$ (the sliding constraint).

Keywords

characteristic of a constraint: hypergraph.

combinatorial object: sequence.

constraint type: sliding sequence constraint, soft constraint, relaxation.

Arc input(s)

$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$

Arc generator

𝑃𝐴𝑇𝐻

\mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗

Arc arity

𝚂𝙴𝚀

Arc constraint(s)

•

𝚜𝚞𝚖_𝚌𝚝𝚛

(𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗, \geq, 𝙻𝙾𝚆)

•

𝚜𝚞𝚖_𝚌𝚝𝚛

(𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗, \leq, 𝚄𝙿)

Graph property(ies)

•

𝐍𝐀𝐑𝐂

\geq 𝙰𝚃𝙻𝙴𝙰𝚂𝚃

•

𝐍𝐀𝐑𝐂

\leq 𝙰𝚃𝙼𝙾𝚂𝚃

Graph model

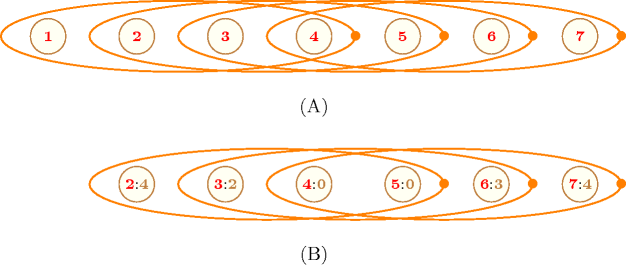
Parts (A) and (B) of Figure 5.331.1 respectively show the initial and final graph associated with the Example slot. For each vertex of the graph we show its corresponding position within the collection of variables. The constraint associated with each arc corresponds to a conjunction of two $𝚜𝚞𝚖_𝚌𝚝𝚛$ constraints involving 4 consecutive variables. In Part (B), we did not put vertex 1 since the single arc constraint that mentions vertex 1 does not hold (i.e., the sum $2 + 4 + 2 + 0 = 8$ is not located in interval $[3, 7]$ ). However, the directed hypergraph contains 3 arcs, so the $𝚛𝚎𝚕𝚊𝚡𝚎𝚍_𝚜𝚕𝚒𝚍𝚒𝚗𝚐_𝚜𝚞𝚖$ constraint is satisfied since it was requested to have between 3 and 4 arcs.

Figure 5.331.1. (A) Initial and (B) final graph of the $𝚛𝚎𝚕𝚊𝚡𝚎𝚍_𝚜𝚕𝚒𝚍𝚒𝚗𝚐_𝚜𝚞𝚖$ $(3, 4, 3, 7, 4, 〈 2, 4, 2, 0, 0, 3, 4 〉)$ constraint of the Example slot where each ellipse represents an hyperedge involving $𝚂𝙴𝚀 = 4$ vertices (e.g., the rightmost ellipse represents the constraint $0 + 0 + 3 + 4 \in [3, 7]$ )

Global Constraint Catalog

5. Global Constraint Catalogue

5.331. relaxed_sliding_sum