5.49. balance_tree
| DESCRIPTION | LINKS | GRAPH |
- Origin
- Constraint
- Arguments
- Restrictions
- Purpose
Consider a digraph described by the collection. Partition into a set of vertex disjoint trees in such a way that each vertex of belongs to a single tree. is equal to the difference between the number of vertices of the largest tree and the number of vertices of the smallest tree.
- Example
-
In the first example we have two trees involving respectively the set of vertices and the set . They are depicted by Figure 5.49.1. Since is the difference between the number of vertices of the largest tree (i.e., 6) and the number of vertices of the smallest tree (i.e., 2) the corresponding constraint holds.
Figure 5.49.1. The two trees associated with the first example of the Example slot, respectively containing 6 and 2 vertices, therefore ; each vertex contains the information where is the index of its father in the tree (by convention the father of the root is the root itself).
- All solutions
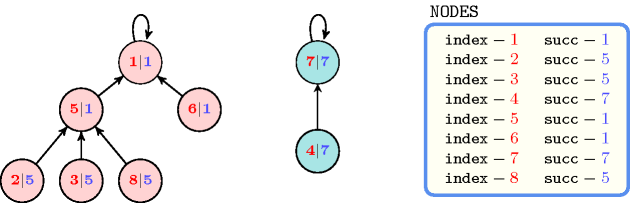
Figure 5.49.2 gives all solutions to the following non ground instance of the constraint: , , , , , , , .
Figure 5.49.2. All solutions corresponding to the non ground example of the constraint of the All solutions slot; the attribute is displayed as indices of the attribute and all vertices of a same tree are coloured by the same colour.

- Typical
- Symmetry
Items of are permutable.
- Arg. properties
Functional dependency: determined by .
- Counting
-
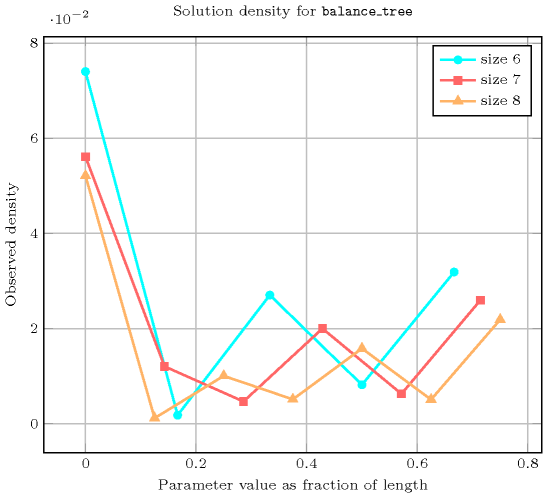
Length () 2 3 4 5 6 7 8 Solutions 3 16 125 1296 16807 262144 4782969 Number of solutions for : domains
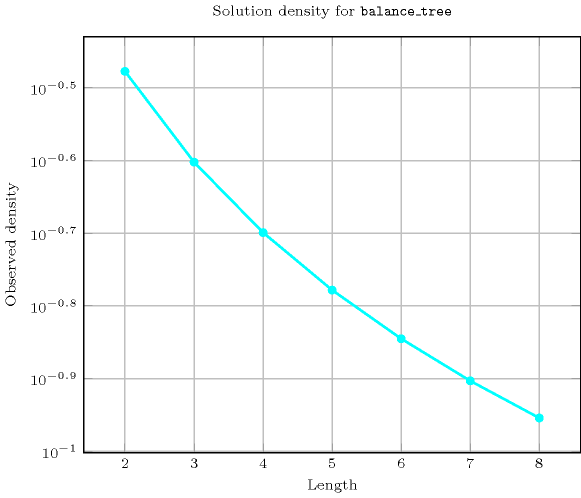
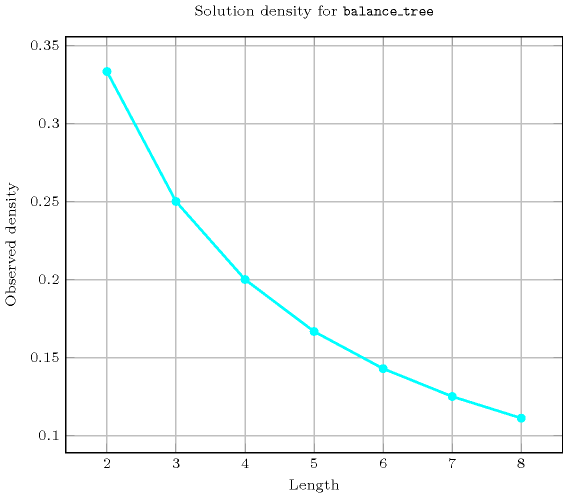
Length () 2 3 4 5 6 7 8 Total 3 16 125 1296 16807 262144 4782969 Parameter value 0 3 10 77 626 8707 117650 2242193 1 - 6 12 260 210 25242 49616 2 - - 36 90 3180 9765 432264 3 - - - 320 960 41930 219520 4 - - - - 3750 13125 680456 5 - - - - - 54432 217728 6 - - - - - - 941192 Solution count for : domains
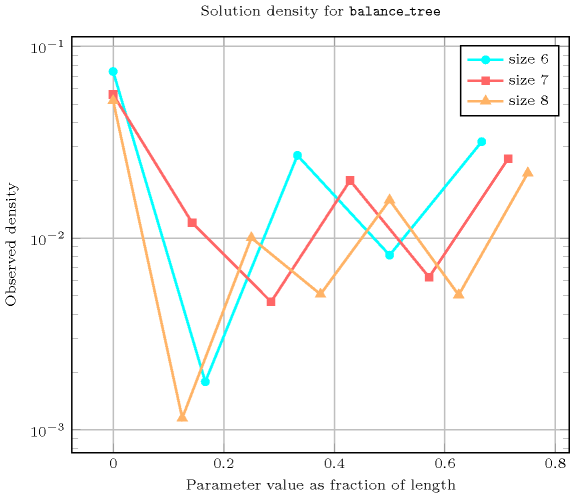
- See also
-
related: (equivalence classes correspond to vertices in same tree rather than variables assigned to the same value), (do not care how many trees but how balanced the trees are).
- Keywords
constraint type: graph constraint, graph partitioning constraint.
- Cond. implications
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
- Graph property(ies)
-
- Graph model
In order to express the binary constraint that links two vertices one has to make explicit the identifier of the vertices. This is why the constraint considers objects that have two attributes:
One fixed attribute that is the identifier of the vertex,
One variable attribute that is the successor of the vertex.
We use the graph property in order to specify the fact that the size of the largest strongly connected component should not exceed one. In fact each root of a tree is a strongly connected component with a single vertex.
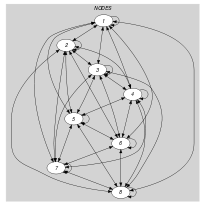
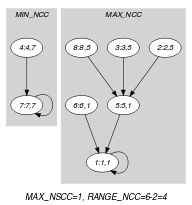
Parts (A) and (B) of Figure 5.49.3 respectively show the initial and final graph associated with the first example of the Example slot. Since we use the graph property, we show the connected components of the final graph. The constraint holds since all the vertices belong to a tree and since .
Figure 5.49.3. Initial and final graph of the constraint
(a) (b)