5.173. group_skip_isolated_item
| DESCRIPTION | LINKS | GRAPH | AUTOMATON |
- Origin
- Constraint
- Arguments
- Restrictions
- Purpose
Let be the number of variables of the collection . Let be consecutive variables of the collection of variables such that the following conditions apply:
All variables take their value in the set of values ,
or does not take a value in ,
or does not take a value in .
We call such a set of variables a group. The constraint is true if all the following conditions hold:
There are exactly groups of variables,
The number of variables of the smallest group is ,
The number of variables of the largest group is ,
The number of variables that take their value in the set of values is equal to .
- Example
-
Given the fact that groups are formed by even values in (i.e., values expressed by the collection), and the fact that isolated even values are ignored, the constraint holds since:
Its first argument, , is set to value 1 since the sequence contains only one group of even values involving more than one even value (i.e., group ).
Its second and third arguments, and , are both set to 2 since the only group of even values with more than one even value involves two values (i.e., group ).
The fourth argument, , is fixed to 2 since it corresponds to the total number of even values belonging to groups involving more than one even value (i.e., value 4 is discarded since it is an isolated even value of the sequence ).
- Typical
- Symmetries
Items of can be reversed.
Items of are permutable.
An occurrence of a value of that belongs to (resp. does not belong to ) can be replaced by any other value in (resp. not in ).
- Arg. properties
Functional dependency: determined by and .
Functional dependency: determined by and .
Functional dependency: determined by and .
Functional dependency: determined by and .
- Usage
This constraint is useful in order to specify rules about how rest days should be allocated to a person during a period of consecutive days. In this case are the codes for the rest days (perhaps a single value) and corresponds to the amount of work done during consecutive days. We can then express a rule like: in a month one should have at least 4 periods of at least 2 rest days (isolated rest days are not counted as rest periods).
- Remark
The following invariant imposes a limit on the maximum number of groups wrt the minimum size of a group and the total number of variables: .
- See also
- Keywords
characteristic of a constraint: automaton, automaton with counters, automaton with same input symbol.
combinatorial object: sequence.
constraint arguments: reverse of a constraint.
constraint network structure: alpha-acyclic constraint network(2), alpha-acyclic constraint network(3).
constraint type: timetabling constraint.
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
-
- Graph property(ies)
-
- Graph model
We use the arc generator in order to produce the initial graph. In the context of the Example slot, this creates the graph depicted in part (A) of Figure 5.173.1. We use together with the arc constraint in order to skip the isolated variables that take a value in that we do not want to count as a group. This is why, on the example, value 4 is not counted as a group. Part (B) of Figure 5.173.1 shows the final graph associated with the Example slot. The constraint of the Example slot holds since:
The final graph contains one strongly connected component. Therefore the number of groups is equal to one.
The unique strongly connected component of the final graph contains two vertices. Therefore and are both equal to 2.
The number of vertices of the final graph is equal to two. Therefore is equal to 2.
Figure 5.173.1. Initial and final graph of the constraint
(a) (b)
- Automaton
Figures 5.173.2, 5.173.4, 5.173.6 and 5.173.8 depict the different automata associated with the constraint. For the automata that respectively compute , , and we have a 0-1 signature variable for each variable of the collection . The following signature constraint links and : .
Figure 5.173.2. Automaton for the argument of the constraint and its glue matrix
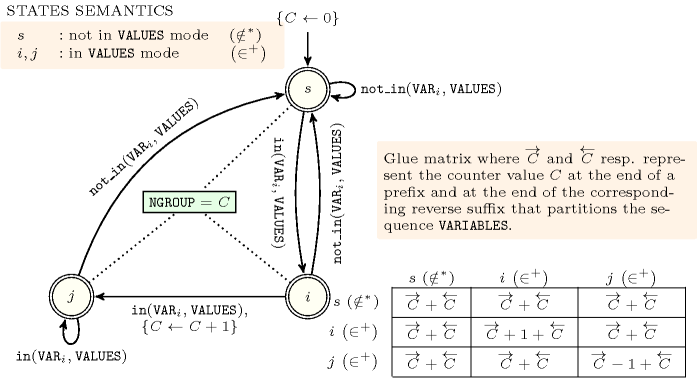
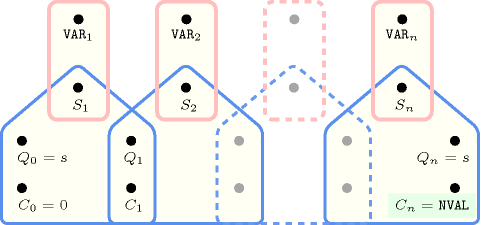
Figure 5.173.3. Hypergraph of the reformulation corresponding to the automaton (with one counter) of the argument of the constraint (since all states of the automaton are accepting there is no restriction on the last variable )
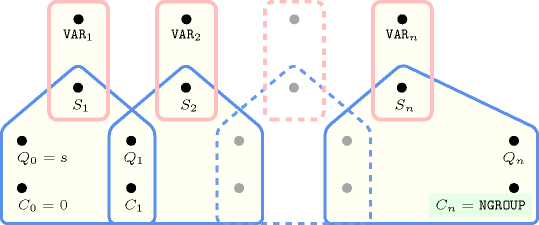
Figure 5.173.4. Automaton for the argument of the constraint and its glue matrix
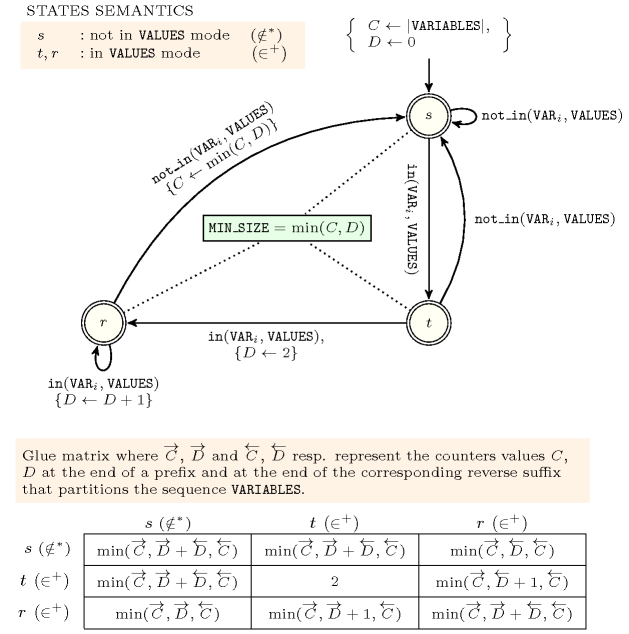
Figure 5.173.5. Hypergraph of the reformulation corresponding to the automaton (with two counters) of the argument of the constraint where stands for (since all states of the automaton are accepting there is no restriction on the last variable )
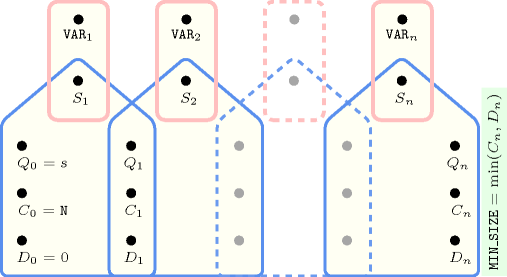
Figure 5.173.6. Automaton for the argument of the constraint and its glue matrix
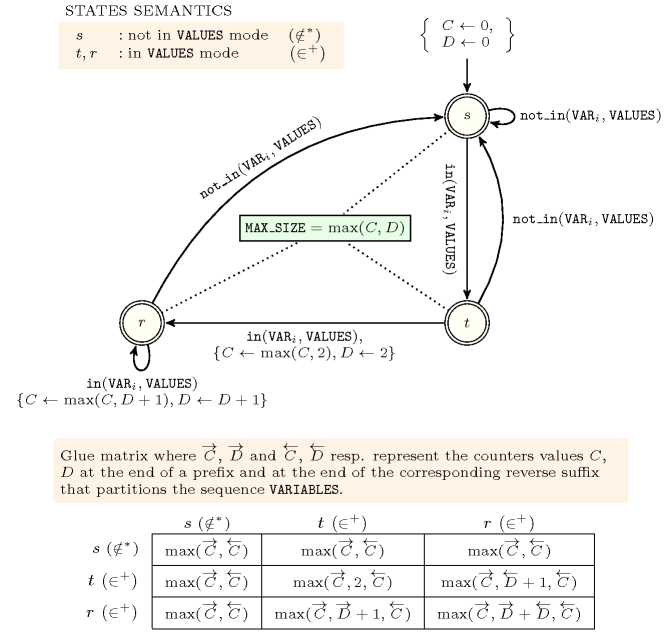
Figure 5.173.7. Hypergraph of the reformulation corresponding to the automaton (with two counters) of the argument of the constraint (since all states of the automaton are accepting there is no restriction on the last variable )
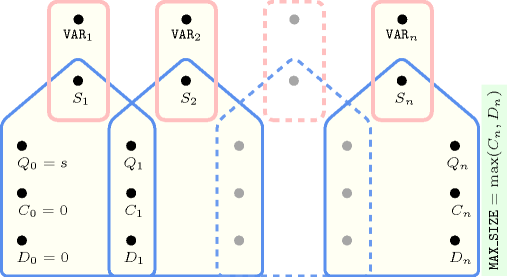
Figure 5.173.8. Automaton for the argument of the constraint and its glue matrix

Figure 5.173.9. Hypergraph of the reformulation corresponding to the automaton (with one counter) of the argument of the constraint