Global Constraint Catalog: Cused_by

5.413. used_by_interval

DESCRIPTION

LINKS

GRAPH

Origin

Derived from $𝚞𝚜𝚎𝚍_𝚋𝚢$ .

Constraint

$𝚞𝚜𝚎𝚍_𝚋𝚢_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2, 𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻)$

Arguments

$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)$
$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)$
$𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻$	$𝚒𝚗𝚝$

Restrictions

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 | \geq | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 |

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1, 𝚟𝚊𝚛)

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2, 𝚟𝚊𝚛)

𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 > 0

Purpose

Let $N_{i}$ (respectively $M_{i}$ ) denote the number of variables of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ (respectively $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ ) that take a value in the interval $[𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 \cdot i, 𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 \cdot i + 𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 - 1]$ . For all integer $i$ we have $M_{i} > 0 \Rightarrow N_{i} \geq M_{i}$ .

Example

(〈1, 9, 1, 8, 6, 2〉, 〈1, 0, 7, 7〉, 3)

In the example, the third argument $𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 = 3$ defines the following family of intervals $[3 \cdot k, 3 \cdot k + 2]$ , where $k$ is an integer. Consequently the values of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 = 〈 1, 0, 7, 7 〉$ are respectively located within intervals $[0, 2]$ , $[0, 2]$ , $[6, 8]$ , $[6, 8]$ . Therefore intervals $[0, 2]$ and $[6, 8]$ are respectively used 2 and 2 times.

Similarly, the values of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 = 〈 1, 9, 1, 8, 6, 2 〉$ are respectively located within intervals $[0, 2]$ , $[9, 11]$ , $[0, 2]$ , $[6, 8]$ , $[6, 8]$ , $[0, 2]$ . Therefore intervals $[0, 2]$ , $[6, 8]$ and $[9, 11]$ are respectively used 3, 2 and 1 times.

Consequently, the $𝚞𝚜𝚎𝚍_𝚋𝚢_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕$ constraint holds since, for each interval associated with the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 = 〈 1, 0, 7, 7 〉$ , its number of occurrences within $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 = 〈 1, 9, 1, 8, 6, 2 〉$ is greater than or equal to its number of occurrences within $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ :

Interval $[0, 2]$ occurs 3 times within $〈 1, 9, 1, 8, 6, 2 〉$ and 2 times within $〈 1, 0, 7, 7 〉$ .
Interval $[6, 8]$ occurs 2 times within $〈 1, 9, 1, 8, 6, 2 〉$ and 2 times within $〈 1, 0, 7, 7 〉$ .

Typical

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 | > 1

𝚛𝚊𝚗𝚐𝚎

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 . 𝚟𝚊𝚛) > 1

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 | > 1

𝚛𝚊𝚗𝚐𝚎

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 . 𝚟𝚊𝚛) > 1

𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 > 1

𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 <

𝚛𝚊𝚗𝚐𝚎

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 . 𝚟𝚊𝚛)

𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 <

𝚛𝚊𝚗𝚐𝚎

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 . 𝚟𝚊𝚛)

Symmetries

Items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ are permutable.
Items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ are permutable.
An occurrence of a value of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 . 𝚟𝚊𝚛$ that belongs to the $k$ -th interval, of size $𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻$ , can be replaced by any other value of the same interval.
An occurrence of a value of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 . 𝚟𝚊𝚛$ that belongs to the $k$ -th interval, of size $𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻$ , can be replaced by any other value of the same interval.

Arg. properties

Contractible wrt. $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ .
Extensible wrt. $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ .
Aggregate: $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 (𝚞𝚗𝚒𝚘𝚗)$ , $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 (𝚞𝚗𝚒𝚘𝚗)$ , $𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 (𝚒𝚍)$ .

Reformulation

The $𝚞𝚜𝚎𝚍_𝚋𝚢_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕$ $(〈 𝚟𝚊𝚛 - U_{1} 𝚟𝚊𝚛 - U_{2}, \dots, 𝚟𝚊𝚛 - U_{| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 |} 〉, 〈 𝚟𝚊𝚛 - V_{1} 𝚟𝚊𝚛 - V_{2}, \dots, 𝚟𝚊𝚛 - V_{| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 |} 〉, 𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻)$ constraint can be expressed by introducing $| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 | + | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 |$ quotient variables

$U_{i} = 𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 \cdot P_{i} + R_{i}$ , $R_{i} \in [0, 𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 - 1]$ $(i \in [1, | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 |])$ ,

$V_{i} = 𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 \cdot Q_{i} + S_{i}$ , $S_{i} \in [0, 𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 - 1]$ $(i \in [1, | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 |])$ ,

in term of a conjunction of $| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 |$ reified constraints of the form:

$\sum_{1 \leq j \leq | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 |} (Q_{i} = P_{j}) \geq \sum_{1 \leq j \leq | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 |} (Q_{i} = Q_{j})$ $(i \in [1, | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 |])$ .

Used in

$𝚔_𝚞𝚜𝚎𝚍_𝚋𝚢_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕$ .

See also

implied by: $𝚜𝚊𝚖𝚎_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕$ .

soft variant: $𝚜𝚘𝚏𝚝_𝚞𝚜𝚎𝚍_𝚋𝚢_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕_𝚟𝚊𝚛$ (variable-based violation measure).

specialisation: $𝚞𝚜𝚎𝚍_𝚋𝚢$ ( $𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎 / 𝚌𝚘𝚗𝚜𝚝𝚊𝚗𝚝$ replaced by $𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎$ ).

system of constraints: $𝚔_𝚞𝚜𝚎𝚍_𝚋𝚢_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕$ .

Keywords

characteristic of a constraint: sort based reformulation.

constraint arguments: constraint between two collections of variables.

modelling: inclusion, interval.

Arc input(s)

$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$

Arc generator

𝑃𝑅𝑂𝐷𝑈𝐶𝑇

\mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1, 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2)

Arc arity

Arc constraint(s)

\begin{matrix} 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1 . 𝚟𝚊𝚛 / 𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 = \\ 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2 . 𝚟𝚊𝚛 / 𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 \end{matrix}

Graph property(ies)

• for all connected components:

𝐍𝐒𝐎𝐔𝐑𝐂𝐄

\geq

𝐍𝐒𝐈𝐍𝐊

•

𝐍𝐒𝐈𝐍𝐊

= | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 |

Graph model

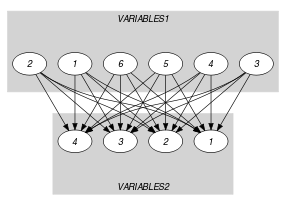
Parts (A) and (B) of Figure 5.413.1 respectively show the initial and final graph associated with the Example slot. Since we use the $𝐍𝐒𝐎𝐔𝐑𝐂𝐄$ and $𝐍𝐒𝐈𝐍𝐊$ graph properties, the source and sink vertices of the final graph are stressed with a double circle. Since there is a constraint on each connected component of the final graph we also show the different connected components. Each of them corresponds to an equivalence class according to the arc constraint. Note that the vertex corresponding to the variable that takes value 9 was removed from the final graph since there is no arc for which the associated equivalence constraint holds. The $𝚞𝚜𝚎𝚍_𝚋𝚢_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕$ constraint holds since:

For each connected component of the final graph the number of sources is greater than or equal to the number of sinks.
The number of sinks of the final graph is equal to $| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 |$ .

Figure 5.413.1. Initial and final graph of the $𝚞𝚜𝚎𝚍_𝚋𝚢_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕$ constraint

(a)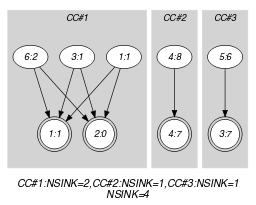

(b)

Signature

Since the initial graph contains only sources and sinks, and since sources of the initial graph cannot become sinks of the final graph, we have that the maximum number of sinks of the final graph is equal to $| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 |$ . Therefore we can rewrite $𝐍𝐒𝐈𝐍𝐊 = | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 |$ to $𝐍𝐒𝐈𝐍𝐊 \geq | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 |$ and simplify $\underset{̲}{\bar{𝐍𝐒𝐈𝐍𝐊}}$ to $\bar{𝐍𝐒𝐈𝐍𝐊}$ .

Global Constraint Catalog

5. Global Constraint Catalogue

5.413. used_by_interval

Figure 5.413.1. Initial and final graph of the 𝚞𝚜𝚎𝚍_𝚋𝚢_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕 constraint

Figure 5.413.1. Initial and final graph of the $𝚞𝚜𝚎𝚍_𝚋𝚢_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕$ constraint