Global Constraint Catalog: Csequence

5.343. sequence_folding

DESCRIPTION

LINKS

GRAPH

AUTOMATON

Origin

J. Pearson

Constraint

$𝚜𝚎𝚚𝚞𝚎𝚗𝚌𝚎_𝚏𝚘𝚕𝚍𝚒𝚗𝚐 (𝙻𝙴𝚃𝚃𝙴𝚁𝚂)$

Argument

𝙻𝙴𝚃𝚃𝙴𝚁𝚂

𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚒𝚗𝚍𝚎𝚡 - 𝚒𝚗𝚝, 𝚗𝚎𝚡𝚝 - 𝚍𝚟𝚊𝚛)

Restrictions

| 𝙻𝙴𝚃𝚃𝙴𝚁𝚂 | \geq 1

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝙻𝙴𝚃𝚃𝙴𝚁𝚂, [𝚒𝚗𝚍𝚎𝚡, 𝚗𝚎𝚡𝚝])

𝙻𝙴𝚃𝚃𝙴𝚁𝚂 . 𝚒𝚗𝚍𝚎𝚡 \geq 1

𝙻𝙴𝚃𝚃𝙴𝚁𝚂 . 𝚒𝚗𝚍𝚎𝚡 \leq | 𝙻𝙴𝚃𝚃𝙴𝚁𝚂 |

𝚒𝚗𝚌𝚛𝚎𝚊𝚜𝚒𝚗𝚐_𝚜𝚎𝚚

(𝙻𝙴𝚃𝚃𝙴𝚁𝚂, 𝚒𝚗𝚍𝚎𝚡)

𝙻𝙴𝚃𝚃𝙴𝚁𝚂 . 𝚗𝚎𝚡𝚝 \geq 1

𝙻𝙴𝚃𝚃𝙴𝚁𝚂 . 𝚗𝚎𝚡𝚝 \leq | 𝙻𝙴𝚃𝚃𝙴𝚁𝚂 |

Purpose

Express the fact that a sequence is folded in a way that no crossing occurs. A sequence is modelled by a collection of letters. For each letter $l_{1}$ of a sequence, we indicate the next letter $l_{2}$ located after $l_{1}$ that is directly in contact with $l_{1}$ ( $l_{1}$ itself if such a letter does not exist).

Example

(\begin{matrix} 〈\begin{matrix} 𝚒𝚗𝚍𝚎𝚡 - 1 & 𝚗𝚎𝚡𝚝 - 1, \\ 𝚒𝚗𝚍𝚎𝚡 - 2 & 𝚗𝚎𝚡𝚝 - 8, \\ 𝚒𝚗𝚍𝚎𝚡 - 3 & 𝚗𝚎𝚡𝚝 - 3, \\ 𝚒𝚗𝚍𝚎𝚡 - 4 & 𝚗𝚎𝚡𝚝 - 5, \\ 𝚒𝚗𝚍𝚎𝚡 - 5 & 𝚗𝚎𝚡𝚝 - 5, \\ 𝚒𝚗𝚍𝚎𝚡 - 6 & 𝚗𝚎𝚡𝚝 - 7, \\ 𝚒𝚗𝚍𝚎𝚡 - 7 & 𝚗𝚎𝚡𝚝 - 7, \\ 𝚒𝚗𝚍𝚎𝚡 - 8 & 𝚗𝚎𝚡𝚝 - 8, \\ 𝚒𝚗𝚍𝚎𝚡 - 9 & 𝚗𝚎𝚡𝚝 - 9 \end{matrix}〉 \end{matrix})

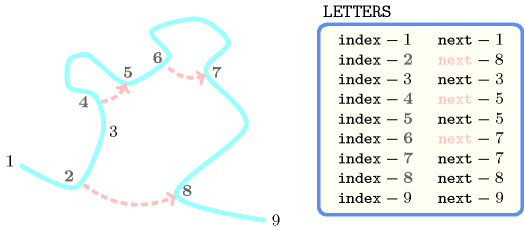
Figure 5.343.1 gives the folded sequence associated with the previous example. Each number represents the index of an item. The $𝚜𝚎𝚚𝚞𝚎𝚗𝚌𝚎_𝚏𝚘𝚕𝚍𝚒𝚗𝚐$ constraint holds since no crossing occurs.

Figure 5.343.1. Folded sequence (in blue) of the Example slot: links from a letter to a distinct letter are represented by a dashed arc, while self-loops are not drawn

Typical

| 𝙻𝙴𝚃𝚃𝙴𝚁𝚂 | > 2

𝚛𝚊𝚗𝚐𝚎

(𝙻𝙴𝚃𝚃𝙴𝚁𝚂 . 𝚗𝚎𝚡𝚝) > 1

Usage

Motivated by RNA folding [FlammHofackerStadler99].

Keywords

application area: bioinformatics.

characteristic of a constraint: automaton, automaton without counters, reified automaton constraint.

combinatorial object: sequence.

constraint type: decomposition.

geometry: geometrical constraint.

Arc input(s)

$𝙻𝙴𝚃𝚃𝙴𝚁𝚂$

Arc generator

𝑆𝐸𝐿𝐹

\mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚕𝚎𝚝𝚝𝚎𝚛𝚜)

Arc arity

Arc constraint(s)

𝚕𝚎𝚝𝚝𝚎𝚛𝚜 . 𝚗𝚎𝚡𝚝 \geq 𝚕𝚎𝚝𝚝𝚎𝚛𝚜 . 𝚒𝚗𝚍𝚎𝚡

Graph property(ies)

𝐍𝐀𝐑𝐂

= | 𝙻𝙴𝚃𝚃𝙴𝚁𝚂 |

Arc input(s)

$𝙻𝙴𝚃𝚃𝙴𝚁𝚂$

Arc generator

𝐶𝐿𝐼𝑄𝑈𝐸

(<) \mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚕𝚎𝚝𝚝𝚎𝚛𝚜 1, 𝚕𝚎𝚝𝚝𝚎𝚛𝚜 2)

Arc arity

Arc constraint(s)

⋁ (\begin{matrix} 𝚕𝚎𝚝𝚝𝚎𝚛𝚜 2 . 𝚒𝚗𝚍𝚎𝚡 \geq 𝚕𝚎𝚝𝚝𝚎𝚛𝚜 1 . 𝚗𝚎𝚡𝚝, \\ 𝚕𝚎𝚝𝚝𝚎𝚛𝚜 2 . 𝚗𝚎𝚡𝚝 \leq 𝚕𝚎𝚝𝚝𝚎𝚛𝚜 1 . 𝚗𝚎𝚡𝚝 \end{matrix})

Graph property(ies)

𝐍𝐀𝐑𝐂

= | 𝙻𝙴𝚃𝚃𝙴𝚁𝚂 | * (| 𝙻𝙴𝚃𝚃𝙴𝚁𝚂 | - 1) / 2

Graph model

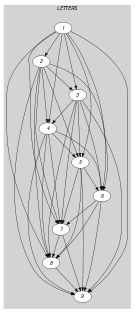
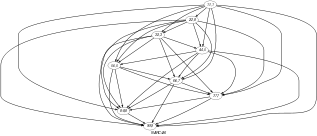
Parts (A) and (B) of Figure 5.343.2 respectively show the initial and final graph associated with the Example slot. Since we use the $𝐍𝐀𝐑𝐂$ graph property, the arcs of the final graph are stressed in bold.

Figure 5.343.2. Initial and final graph of the $𝚜𝚎𝚚𝚞𝚎𝚗𝚌𝚎_𝚏𝚘𝚕𝚍𝚒𝚗𝚐$ constraint


(a)	(b)

Signature

Consider the first graph constraint. Since we use the $𝑆𝐸𝐿𝐹$ arc generator on the $𝙻𝙴𝚃𝚃𝙴𝚁𝚂$ collection the maximum number of arcs of the final graph is equal to $| 𝙻𝙴𝚃𝚃𝙴𝚁𝚂 |$ . Therefore we can rewrite the graph property $𝐍𝐀𝐑𝐂 = | 𝙻𝙴𝚃𝚃𝙴𝚁𝚂 |$ to $𝐍𝐀𝐑𝐂 \geq | 𝙻𝙴𝚃𝚃𝙴𝚁𝚂 |$ and simplify $\underset{̲}{\bar{𝐍𝐀𝐑𝐂}}$ to $\bar{𝐍𝐀𝐑𝐂}$ .

Consider now the second graph constraint. Since we use the $𝐶𝐿𝐼𝑄𝑈𝐸 (<)$ arc generator on the $𝙻𝙴𝚃𝚃𝙴𝚁𝚂$ collection the maximum number of arcs of the final graph is equal to $| 𝙻𝙴𝚃𝚃𝙴𝚁𝚂 | \cdot (| 𝙻𝙴𝚃𝚃𝙴𝚁𝚂 | - 1) / 2$ . Therefore we can rewrite the graph property $𝐍𝐀𝐑𝐂 = | 𝙻𝙴𝚃𝚃𝙴𝚁𝚂 | \cdot (| 𝙻𝙴𝚃𝚃𝙴𝚁𝚂 | - 1) / 2$ to $𝐍𝐀𝐑𝐂 \geq | 𝙻𝙴𝚃𝚃𝙴𝚁𝚂 | \cdot (| 𝙻𝙴𝚃𝚃𝙴𝚁𝚂 | - 1) / 2$ and simplify $\underset{̲}{\bar{𝐍𝐀𝐑𝐂}}$ to $\bar{𝐍𝐀𝐑𝐂}$ .

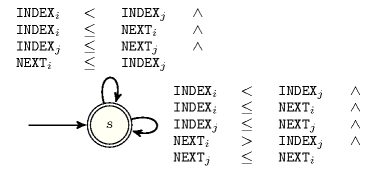
Automaton

Figure 5.343.3 depicts the automaton associated with the $𝚜𝚎𝚚𝚞𝚎𝚗𝚌𝚎_𝚏𝚘𝚕𝚍𝚒𝚗𝚐$ constraint. Consider the $i^{t h}$ and the $j^{t h}$ $(i < j)$ items of the collection $𝙻𝙴𝚃𝚃𝙴𝚁𝚂$ . Let ${𝙸𝙽𝙳𝙴𝚇}_{i}$ and ${𝙽𝙴𝚇𝚃}_{i}$ respectively denote the $𝚒𝚗𝚍𝚎𝚡$ and the $𝚗𝚎𝚡𝚝$ attributes of the $i^{t h}$ item of the collection $𝙻𝙴𝚃𝚃𝙴𝚁𝚂$ . Similarly, let ${𝙸𝙽𝙳𝙴𝚇}_{j}$ and ${𝙽𝙴𝚇𝚃}_{j}$ respectively denote the $𝚒𝚗𝚍𝚎𝚡$ and the $𝚗𝚎𝚡𝚝$ attributes of the $j^{t h}$ item of the collection $𝙻𝙴𝚃𝚃𝙴𝚁𝚂$ . To each quadruple $({𝙸𝙽𝙳𝙴𝚇}_{i}, {𝙽𝙴𝚇𝚃}_{i}, {𝙸𝙽𝙳𝙴𝚇}_{j}, {𝙽𝙴𝚇𝚃}_{j})$ corresponds a signature variable $S_{i, j}$ , which takes its value in ${0, 1, 2}$ , as well as the following signature constraint:

$({𝙸𝙽𝙳𝙴𝚇}_{i} \leq {𝙽𝙴𝚇𝚃}_{i}) \land ({𝙸𝙽𝙳𝙴𝚇}_{j} \leq {𝙽𝙴𝚇𝚃}_{j}) \land ({𝙽𝙴𝚇𝚃}_{i} \leq {𝙽𝙴𝚇𝚃}_{j}) \Leftrightarrow S_{i, j} = 0 \land$

$({𝙸𝙽𝙳𝙴𝚇}_{i} \leq {𝙽𝙴𝚇𝚃}_{i}) \land ({𝙸𝙽𝙳𝙴𝚇}_{j} \leq {𝙽𝙴𝚇𝚃}_{j}) \land ({𝙽𝙴𝚇𝚃}_{i} > {𝙸𝙽𝙳𝙴𝚇}_{j}) \land ({𝙽𝙴𝚇𝚃}_{j} \leq {𝙽𝙴𝚇𝚃}_{i}) \Leftrightarrow S_{i, j} = 1$ .

Figure 5.343.3. Automaton of the $𝚜𝚎𝚚𝚞𝚎𝚗𝚌𝚎_𝚏𝚘𝚕𝚍𝚒𝚗𝚐$ constraint

Global Constraint Catalog

5. Global Constraint Catalogue

5.343. sequence_folding

Figure 5.343.1. Folded sequence (in blue) of the Example slot: links from a letter to a distinct letter are represented by a dashed arc, while self-loops are not drawn

Figure 5.343.2. Initial and final graph of the 𝚜𝚎𝚚𝚞𝚎𝚗𝚌𝚎_𝚏𝚘𝚕𝚍𝚒𝚗𝚐 constraint

Figure 5.343.3. Automaton of the 𝚜𝚎𝚚𝚞𝚎𝚗𝚌𝚎_𝚏𝚘𝚕𝚍𝚒𝚗𝚐 constraint

Figure 5.343.2. Initial and final graph of the $𝚜𝚎𝚚𝚞𝚎𝚗𝚌𝚎_𝚏𝚘𝚕𝚍𝚒𝚗𝚐$ constraint

Figure 5.343.3. Automaton of the $𝚜𝚎𝚚𝚞𝚎𝚗𝚌𝚎_𝚏𝚘𝚕𝚍𝚒𝚗𝚐$ constraint