Global Constraint Catalog: Ccycle_card_on

5.104. cycle_card_on_path

DESCRIPTION

LINKS

GRAPH

Origin

CHIP

Constraint

$𝚌𝚢𝚌𝚕𝚎_𝚌𝚊𝚛𝚍_𝚘𝚗_𝚙𝚊𝚝𝚑 (𝙽𝙲𝚈𝙲𝙻𝙴, 𝙽𝙾𝙳𝙴𝚂, 𝙰𝚃𝙻𝙴𝙰𝚂𝚃, 𝙰𝚃𝙼𝙾𝚂𝚃, 𝙿𝙰𝚃𝙷_𝙻𝙴𝙽, 𝚅𝙰𝙻𝚄𝙴𝚂)$

Arguments

$𝙽𝙲𝚈𝙲𝙻𝙴$	$𝚍𝚟𝚊𝚛$
$𝙽𝙾𝙳𝙴𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚒𝚗𝚍𝚎𝚡 - 𝚒𝚗𝚝, 𝚜𝚞𝚌𝚌 - 𝚍𝚟𝚊𝚛, 𝚌𝚘𝚕𝚘𝚞𝚛 - 𝚍𝚟𝚊𝚛)$
$𝙰𝚃𝙻𝙴𝙰𝚂𝚃$	$𝚒𝚗𝚝$
$𝙰𝚃𝙼𝙾𝚂𝚃$	$𝚒𝚗𝚝$
$𝙿𝙰𝚃𝙷_𝙻𝙴𝙽$	$𝚒𝚗𝚝$
$𝚅𝙰𝙻𝚄𝙴𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚕 - 𝚒𝚗𝚝)$

Restrictions

𝙽𝙲𝚈𝙲𝙻𝙴 \geq 1

𝙽𝙲𝚈𝙲𝙻𝙴 \leq | 𝙽𝙾𝙳𝙴𝚂 |

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝙽𝙾𝙳𝙴𝚂, [𝚒𝚗𝚍𝚎𝚡, 𝚜𝚞𝚌𝚌, 𝚌𝚘𝚕𝚘𝚞𝚛])

𝙽𝙾𝙳𝙴𝚂 . 𝚒𝚗𝚍𝚎𝚡 \geq 1

𝙽𝙾𝙳𝙴𝚂 . 𝚒𝚗𝚍𝚎𝚡 \leq | 𝙽𝙾𝙳𝙴𝚂 |

𝚍𝚒𝚜𝚝𝚒𝚗𝚌𝚝

(𝙽𝙾𝙳𝙴𝚂, 𝚒𝚗𝚍𝚎𝚡)

𝙽𝙾𝙳𝙴𝚂 . 𝚜𝚞𝚌𝚌 \geq 1

𝙽𝙾𝙳𝙴𝚂 . 𝚜𝚞𝚌𝚌 \leq | 𝙽𝙾𝙳𝙴𝚂 |

𝙰𝚃𝙻𝙴𝙰𝚂𝚃 \geq 0

𝙰𝚃𝙻𝙴𝙰𝚂𝚃 \leq 𝙿𝙰𝚃𝙷_𝙻𝙴𝙽

𝙰𝚃𝙼𝙾𝚂𝚃 \geq 𝙰𝚃𝙻𝙴𝙰𝚂𝚃

𝙿𝙰𝚃𝙷_𝙻𝙴𝙽 \geq 0

| 𝚅𝙰𝙻𝚄𝙴𝚂 | \geq 1

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝙻𝚄𝙴𝚂, 𝚟𝚊𝚕)

𝚍𝚒𝚜𝚝𝚒𝚗𝚌𝚝

(𝚅𝙰𝙻𝚄𝙴𝚂, 𝚟𝚊𝚕)

Purpose

Consider a digraph $G$ described by the $𝙽𝙾𝙳𝙴𝚂$ collection. $𝙽𝙲𝚈𝙲𝙻𝙴$ is the number of circuits for covering $G$ in such a way that each vertex belongs to a single circuit. In addition the following constraint must also hold: on each set of $𝙿𝙰𝚃𝙷_𝙻𝙴𝙽$ consecutive distinct vertices of each final circuit, the number of vertices for which the attribute colour takes his value in the collection of values $𝚅𝙰𝙻𝚄𝙴𝚂$ should be located within the range $[𝙰𝚃𝙻𝙴𝙰𝚂𝚃, 𝙰𝚃𝙼𝙾𝚂𝚃]$ .

Example

(\begin{matrix} 2, 〈\begin{matrix} 𝚒𝚗𝚍𝚎𝚡 - 1 & 𝚜𝚞𝚌𝚌 - 7 & 𝚌𝚘𝚕𝚘𝚞𝚛 - 2, \\ 𝚒𝚗𝚍𝚎𝚡 - 2 & 𝚜𝚞𝚌𝚌 - 4 & 𝚌𝚘𝚕𝚘𝚞𝚛 - 3, \\ 𝚒𝚗𝚍𝚎𝚡 - 3 & 𝚜𝚞𝚌𝚌 - 8 & 𝚌𝚘𝚕𝚘𝚞𝚛 - 2, \\ 𝚒𝚗𝚍𝚎𝚡 - 4 & 𝚜𝚞𝚌𝚌 - 9 & 𝚌𝚘𝚕𝚘𝚞𝚛 - 1, \\ 𝚒𝚗𝚍𝚎𝚡 - 5 & 𝚜𝚞𝚌𝚌 - 1 & 𝚌𝚘𝚕𝚘𝚞𝚛 - 2, \\ 𝚒𝚗𝚍𝚎𝚡 - 6 & 𝚜𝚞𝚌𝚌 - 2 & 𝚌𝚘𝚕𝚘𝚞𝚛 - 1, \\ 𝚒𝚗𝚍𝚎𝚡 - 7 & 𝚜𝚞𝚌𝚌 - 5 & 𝚌𝚘𝚕𝚘𝚞𝚛 - 1, \\ 𝚒𝚗𝚍𝚎𝚡 - 8 & 𝚜𝚞𝚌𝚌 - 6 & 𝚌𝚘𝚕𝚘𝚞𝚛 - 1, \\ 𝚒𝚗𝚍𝚎𝚡 - 9 & 𝚜𝚞𝚌𝚌 - 3 & 𝚌𝚘𝚕𝚘𝚞𝚛 - 1 \end{matrix}〉, 1, 2, 3, \\ 〈1〉 \end{matrix})

The constraint $𝚌𝚢𝚌𝚕𝚎_𝚌𝚊𝚛𝚍_𝚘𝚗_𝚙𝚊𝚝𝚑$ holds since the vertices of the $𝙽𝙾𝙳𝙴𝚂$ collection correspond to a set of disjoint circuits and since, for each set of 3 (i.e., $𝙿𝙰𝚃𝙷_𝙻𝙴𝙽 = 3$ ) consecutive vertices, colour 1 (i.e., the value provided by the $𝚅𝙰𝙻𝚄𝙴𝚂$ collection) occurs at least once (i.e., $𝙰𝚃𝙻𝙴𝙰𝚂𝚃 = 1$ ) and at most twice (i.e., $𝙰𝚃𝙼𝙾𝚂𝚃 = 2$ ).

Typical

| 𝙽𝙾𝙳𝙴𝚂 | > 2

𝙽𝙲𝚈𝙲𝙻𝙴 < | 𝙽𝙾𝙳𝙴𝚂 |

𝙰𝚃𝙻𝙴𝙰𝚂𝚃 < 𝙿𝙰𝚃𝙷_𝙻𝙴𝙽

𝙰𝚃𝙼𝙾𝚂𝚃 > 0

𝙿𝙰𝚃𝙷_𝙻𝙴𝙽 > 1

| 𝙽𝙾𝙳𝙴𝚂 | > | 𝚅𝙰𝙻𝚄𝙴𝚂 |

𝙰𝚃𝙻𝙴𝙰𝚂𝚃 > 0 \lor 𝙰𝚃𝙼𝙾𝚂𝚃 < 𝙿𝙰𝚃𝙷_𝙻𝙴𝙽

Symmetries

Items of $𝙽𝙾𝙳𝙴𝚂$ are permutable.
An occurrence of a value of $𝙽𝙾𝙳𝙴𝚂 . 𝚌𝚘𝚕𝚘𝚞𝚛$ that belongs to $𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚟𝚊𝚕$ (resp. does not belong to $𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚟𝚊𝚕$ ) can be replaced by any other value in $𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚟𝚊𝚕$ (resp. not in $𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚟𝚊𝚕$ ).
$𝙰𝚃𝙻𝙴𝙰𝚂𝚃$ can be decreased to any value $\geq 0$ .
$𝙰𝚃𝙼𝙾𝚂𝚃$ can be increased.
Items of $𝚅𝙰𝙻𝚄𝙴𝚂$ are permutable.

Usage

Assume that the vertices of $G$ are partitioned into the following two categories:

Clients to visit.
Depots where one can reload a vehicle.

Using the $𝚌𝚢𝚌𝚕𝚎_𝚌𝚊𝚛𝚍_𝚘𝚗_𝚙𝚊𝚝𝚑$ constraint we can express a constraint like: after visiting three consecutive clients we should visit a depot. This is typically not possible with the $𝚊𝚝𝚖𝚘𝚜𝚝$ constraint since we do not know in advance the set of variables involved in the $𝚊𝚝𝚖𝚘𝚜𝚝$ constraint.

Remark

This constraint is a special case of the $𝚜𝚎𝚚𝚞𝚎𝚗𝚌𝚎$ parameter of the $𝚌𝚢𝚌𝚕𝚎$ constraint of CHIP [Bourreau99].

used in graph description: $𝚊𝚖𝚘𝚗𝚐_𝚕𝚘𝚠_𝚞𝚙$ .

Keywords

characteristic of a constraint: coloured.

combinatorial object: sequence.

constraint type: graph constraint, graph partitioning constraint, sliding sequence constraint.

final graph structure: connected component, one_succ.

Arc input(s)

$𝙽𝙾𝙳𝙴𝚂$

Arc generator

𝐶𝐿𝐼𝑄𝑈𝐸

\mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚗𝚘𝚍𝚎𝚜 1, 𝚗𝚘𝚍𝚎𝚜 2)

Arc arity

Arc constraint(s)

𝚗𝚘𝚍𝚎𝚜 1 . 𝚜𝚞𝚌𝚌 = 𝚗𝚘𝚍𝚎𝚜 2 . 𝚒𝚗𝚍𝚎𝚡

Graph property(ies)

•

𝐍𝐓𝐑𝐄𝐄

= 0

•

𝐍𝐂𝐂

= 𝙽𝙲𝚈𝙲𝙻𝙴

Graph class

𝙾𝙽𝙴_𝚂𝚄𝙲𝙲

Sets

\begin{matrix} 𝖯𝖠𝖳𝖧_𝖫𝖤𝖭𝖦𝖳𝖧 (𝙿𝙰𝚃𝙷_𝙻𝙴𝙽) \mapsto \\ [\begin{matrix} 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 - 𝚌𝚘𝚕 (\begin{matrix} 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 - 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛), \\ 𝚒𝚝𝚎𝚖 (𝚟𝚊𝚛 - 𝙽𝙾𝙳𝙴𝚂 . 𝚌𝚘𝚕𝚘𝚞𝚛)] \end{matrix}) \end{matrix}] \end{matrix}

Constraint(s) on sets

𝚊𝚖𝚘𝚗𝚐_𝚕𝚘𝚠_𝚞𝚙

(𝙰𝚃𝙻𝙴𝙰𝚂𝚃, 𝙰𝚃𝙼𝙾𝚂𝚃, 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜, 𝚅𝙰𝙻𝚄𝙴𝚂)

Graph model

Parts (A) and (B) of Figure 5.104.1 respectively show the initial and final graph associated with the Example slot. Since we use the $𝐍𝐂𝐂$ graph property, we show the two connected components of the final graph. The constraint $𝚌𝚢𝚌𝚕𝚎_𝚌𝚊𝚛𝚍_𝚘𝚗_𝚙𝚊𝚝𝚑$ holds since all the vertices belong to a circuit (i.e., $𝐍𝐓𝐑𝐄𝐄$ $=$ 0) and since for each set of three consecutive vertices, colour 1 occurs at least once and at most twice (i.e., the $𝚊𝚖𝚘𝚗𝚐_𝚕𝚘𝚠_𝚞𝚙$ constraint holds).

Figure 5.104.1. Initial and final graph of the $𝚌𝚢𝚌𝚕𝚎_𝚌𝚊𝚛𝚍_𝚘𝚗_𝚙𝚊𝚝𝚑$ constraint


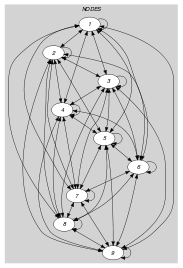
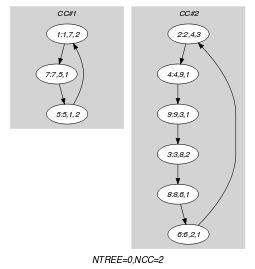
(a)	(b)

Global Constraint Catalog

5. Global Constraint Catalogue

5.104. cycle_card_on_path

Figure 5.104.1. Initial and final graph of the 𝚌𝚢𝚌𝚕𝚎_𝚌𝚊𝚛𝚍_𝚘𝚗_𝚙𝚊𝚝𝚑 constraint

Figure 5.104.1. Initial and final graph of the $𝚌𝚢𝚌𝚕𝚎_𝚌𝚊𝚛𝚍_𝚘𝚗_𝚙𝚊𝚝𝚑$ constraint