5.255. min_index
| DESCRIPTION | LINKS | GRAPH |
- Origin
N. Beldiceanu
- Constraint
- Arguments
- Restrictions
- Purpose
is one of the indices of the collection of variables corresponding to its minimum value.
- Example
-
The attribute of the second and fourth items of the collection is the minimum value over values . Consequently, both constraints hold since their first arguments are respectively set to 2 and 4.
- Typical
- Symmetries
Items of are permutable.
One and the same constant can be added to the attribute of all items of .
- Usage
Within the context of scheduling, assume the variables of the collection correspond to the starts of a set of tasks. Then gives the indexes of those tasks that can be scheduled first.
- See also
- Keywords
characteristic of a constraint: minimum.
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
- Graph property(ies)
-
- Graph model
Parts (A) and (B) of Figure 5.255.1 respectively show the initial and final graph associated with the two examples of the Example slot. Since we use the graph property, the vertices of rank 0 (without considering the loops) of the final graph are outlined with a thick circle.
Figure 5.255.1. Initial and final graph of the constraint
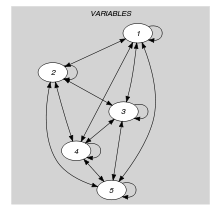
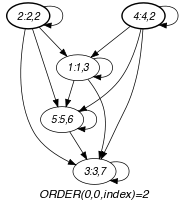
(a) (b)