Global Constraint Catalog: Cbalance

5.45. balance_interval

DESCRIPTION

LINKS

GRAPH

AUTOMATON

Origin

Derived from $𝚋𝚊𝚕𝚊𝚗𝚌𝚎$ .

Constraint

$𝚋𝚊𝚕𝚊𝚗𝚌𝚎_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕 (𝙱𝙰𝙻𝙰𝙽𝙲𝙴, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻)$

Arguments

$𝙱𝙰𝙻𝙰𝙽𝙲𝙴$	$𝚍𝚟𝚊𝚛$
$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)$
$𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻$	$𝚒𝚗𝚝$

Restrictions

𝙱𝙰𝙻𝙰𝙽𝙲𝙴 \geq 0

𝙱𝙰𝙻𝙰𝙽𝙲𝙴 \leq 𝚖𝚊𝚡 (0, | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | - 2)

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚟𝚊𝚛)

𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 > 0

Purpose

Consider the largest set $𝒮_{1}$ (respectively the smallest set $𝒮_{2}$ ) of variables of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ that take their value in a same interval $[𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 \cdot k, 𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 \cdot k + 𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 - 1]$ , where $k$ is an integer. $𝙱𝙰𝙻𝙰𝙽𝙲𝙴$ is equal to the difference between the cardinality of $𝒮_{2}$ and the cardinality of $𝒮_{1}$ .

Example

(3, 〈6, 4, 3, 3, 4〉, 3)

In the example, the third argument $𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 = 3$ defines the following family of intervals $[3 \cdot k, 3 \cdot k + 2]$ , where $k$ is an integer. Values 6,4,3,3 and 4 are respectively located within intervals $[6, 8]$ , $[3, 5]$ , $[3, 5]$ , $[3, 5]$ and $[3, 5]$ . Therefore intervals $[6, 8]$ and $[3, 5]$ are respectively used 1 and 4 times. The $𝚋𝚊𝚕𝚊𝚗𝚌𝚎_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕$ constraint holds since its first argument $𝙱𝙰𝙻𝙰𝙽𝙲𝙴$ is assigned to the difference between the maximum and minimum number of the previous occurrences (i.e., $4 - 1$ ).

Typical

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | > 2

𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 > 1

𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 <

𝚛𝚊𝚗𝚐𝚎

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛)

Symmetries

Items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ are permutable.
An occurrence of a value of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛$ that belongs to the $k$ -th interval, of size $𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻$ , can be replaced by any other value of the same interval.

Arg. properties

Functional dependency: $𝙱𝙰𝙻𝙰𝙽𝙲𝙴$ determined by $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ and $𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻$ .

Usage

An application of the $𝚋𝚊𝚕𝚊𝚗𝚌𝚎_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕$ constraint is to enforce a balanced assignment of interval of values, no matter how many distinct interval of values will be used. In this case one will push down the maximum value of the first argument of the $𝚋𝚊𝚕𝚊𝚗𝚌𝚎_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕$ constraint.

See also

specialisation: $𝚋𝚊𝚕𝚊𝚗𝚌𝚎$ ( $𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎 / 𝚌𝚘𝚗𝚜𝚝𝚊𝚗𝚝$ replaced by $𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎$ ).

Keywords

application area: assignment.

characteristic of a constraint: automaton, automaton with array of counters.

constraint arguments: pure functional dependency.

constraint type: value constraint.

final graph structure: equivalence.

modelling: interval, balanced assignment, functional dependency.

Arc input(s)

$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$

Arc generator

𝐶𝐿𝐼𝑄𝑈𝐸

\mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1, 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2)

Arc arity

Arc constraint(s)

\begin{matrix} 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1 . 𝚟𝚊𝚛 / 𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 = \\ 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2 . 𝚟𝚊𝚛 / 𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 \end{matrix}

Graph property(ies)

𝐑𝐀𝐍𝐆𝐄_𝐍𝐒𝐂𝐂

= 𝙱𝙰𝙻𝙰𝙽𝙲𝙴

Graph class

𝙴𝚀𝚄𝙸𝚅𝙰𝙻𝙴𝙽𝙲𝙴

Graph model

The graph property $𝐑𝐀𝐍𝐆𝐄_𝐍𝐒𝐂𝐂$ constraints the difference between the sizes of the largest and smallest strongly connected components.

Parts (A) and (B) of Figure 5.45.1 respectively show the initial and final graph associated with the Example slot. Since we use the $𝐑𝐀𝐍𝐆𝐄_𝐍𝐒𝐂𝐂$ graph property, we show the largest and smallest strongly connected components of the final graph.

Figure 5.45.1. Initial and final graph of the $𝚋𝚊𝚕𝚊𝚗𝚌𝚎_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕$ constraint


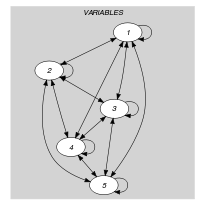
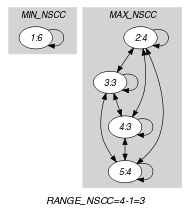
(a)	(b)

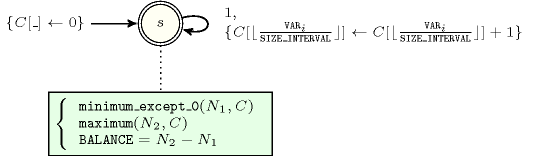
Automaton: Figure 5.45.2 depicts the automaton associated with the $𝚋𝚊𝚕𝚊𝚗𝚌𝚎_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕$ constraint. To each item of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ corresponds a signature variable $S_{i}$ that is equal to 1.

Figure 5.45.2. Automaton of the $𝚋𝚊𝚕𝚊𝚗𝚌𝚎_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕$ constraint

Global Constraint Catalog

5. Global Constraint Catalogue

5.45. balance_interval

Figure 5.45.1. Initial and final graph of the $𝚋𝚊𝚕𝚊𝚗𝚌𝚎_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕$ constraint

Figure 5.45.2. Automaton of the $𝚋𝚊𝚕𝚊𝚗𝚌𝚎_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕$ constraint

Global Constraint Catalog

5. Global Constraint Catalogue

5.45. balance_interval

Figure 5.45.1. Initial and final graph of the 𝚋𝚊𝚕𝚊𝚗𝚌𝚎_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕 constraint

Figure 5.45.2. Automaton of the 𝚋𝚊𝚕𝚊𝚗𝚌𝚎_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕 constraint

Figure 5.45.1. Initial and final graph of the $𝚋𝚊𝚕𝚊𝚗𝚌𝚎_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕$ constraint

Figure 5.45.2. Automaton of the $𝚋𝚊𝚕𝚊𝚗𝚌𝚎_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕$ constraint