5.62. change_continuity
| DESCRIPTION | LINKS | GRAPH | AUTOMATON |
- Origin
N. Beldiceanu
- Constraint
- Arguments
- Restrictions
- Purpose
On the one hand a change is defined by the fact that constraint holds.
On the other hand a continuity is defined by the fact that constraint does not hold.
A period of change on variables
is defined by the fact that all constraints hold for .
A period of continuity on variables
is defined by the fact that all constraints do not hold for .
The constraint holds if and only if:
is equal to the number of periods of change,
is equal to the number of periods of continuity,
is equal to the number of variables of the smallest period of change,
is equal to the number of variables of the largest period of change,
is equal to the number of variables of the smallest period of continuity,
is equal to the number of variables of the largest period of continuity,
is equal to the total number of changes,
is equal to the total number of continuities.
- Example
-
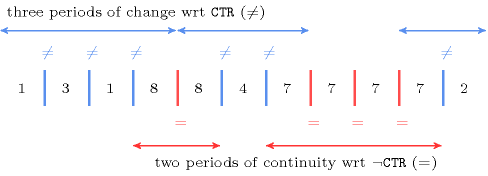
Figure 5.62.1 makes clear the different parameters that are associated with the given example for the collection . We place character | for representing a change and a blank for a continuity. On top of the solution we represent the different periods of change, while below we show the different periods of continuity. The constraint holds since:
Its number of periods of change is equal to 3 (i.e., the 3 periods depicted on top of Figure 5.62.1),
Its number of periods of continuity is equal to 2 (i.e., the 2 periods depicted below Figure 5.62.1),
The number of variables of its smallest period of change is equal to 2 (i.e., the number of variables involved in the third period of change depicted on top of Figure 5.62.1),
The number of variables of the largest period of change is equal to 4 (i.e., the number of variables involved in the first period of change depicted on top of Figure 5.62.1),
The number of variables of the smallest period of continuity is equal to 2 (i.e., the number of variables involved in the first period depicted below Figure 5.62.1),
The number of variables of the largest period of continuity is equal to 4 (i.e., the number of variables involved in the second period depicted below Figure 5.62.1),
The total number of changes is equal to 6 (i.e., the number of occurrences of character | in Figure 5.62.1),
The total number of continuities is equal to 4.
Figure 5.62.1. Illustration of the Example slot: periods of changes and periods of continuities wrt the constraint equal to
- Typical
- Symmetry
One and the same constant can be added to the attribute of all items of .
- Arg. properties
Functional dependency: determined by and .
Functional dependency: determined by and .
Functional dependency: determined by and .
Functional dependency: determined by and .
Functional dependency: determined by and .
Functional dependency: determined by and .
Functional dependency: determined by and .
Functional dependency: determined by and .
- Remark
If the variables of the collection have to take distinct values between 1 and the total number of variables, we have what is called a permutation. In this case, if we choose the binary constraint , then gives the size of the longest run of the permutation; A run is a maximal increasing contiguous subsequence in a permutation.
- See also
- Keywords
characteristic of a constraint: automaton, automaton with counters, automaton with same input symbol.
combinatorial object: sequence, run of a permutation, permutation.
constraint arguments: reverse of a constraint.
constraint network structure: sliding cyclic(1) constraint network(2), sliding cyclic(1) constraint network(3).
constraint type: timetabling constraint.
final graph structure: connected component, apartition, acyclic, bipartite, no loop.
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
- Graph property(ies)
-
- Graph class
-
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
- Graph property(ies)
-
- Graph class
-
- Graph model
We use two graph constraints to respectively catch the constraints on the period of changes and of the period of continuities. In both case each period corresponds to a connected component of the final graph.
Parts (A) and (B) of Figure 5.62.2 respectively show the initial and final graph associated with the first graph constraint of the Example slot.
Figure 5.62.2. Initial and final graph of the constraint
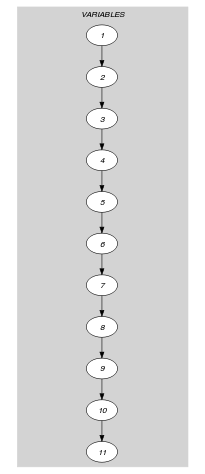
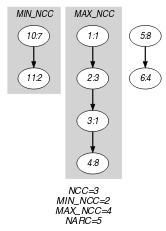
(a) (b)
- Automaton
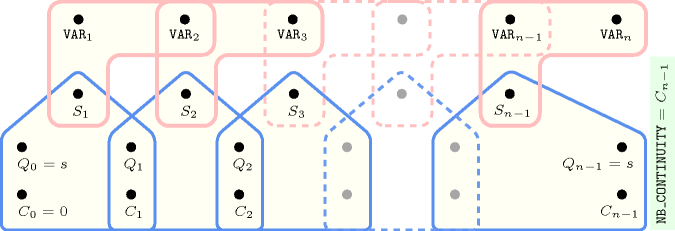
Figures 5.62.3 , 5.62.4 , 5.62.7 , 5.62.8 , 5.62.11 , 5.62.12 and 5.62.15 depict the automata associated with the different graph parameters of the constraint. For the automata that respectively compute , , , and we have a 0-1 signature variable for each pair of consecutive variables of the collection . The following signature constraint links , and : .
Figure 5.62.3. Automaton for the argument of the constraint and its glue matrix; note that the reverse of with is the same constraint, while the reverse with (resp. ) is (resp. ).
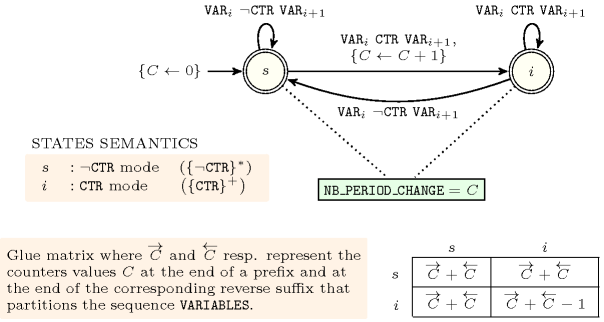
Figure 5.62.4. Automaton for the argument of the constraint and its glue matrix; note that the reverse of with is the same constraint, while the reverse with (resp. ) is (resp. ).
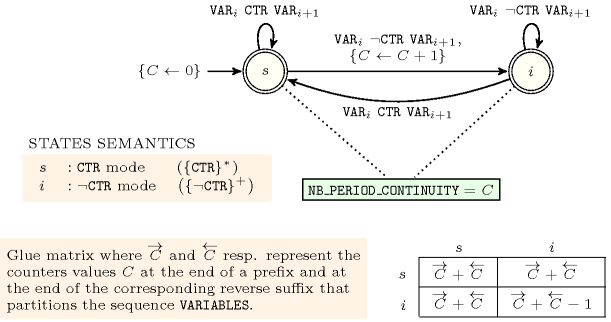
Figure 5.62.5. Hypergraph of the reformulation corresponding to the automaton of the argument of the constraint
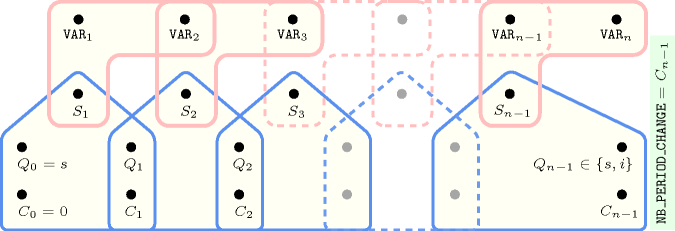
Figure 5.62.6. Hypergraph of the reformulation corresponding to the automaton of the argument of the constraint
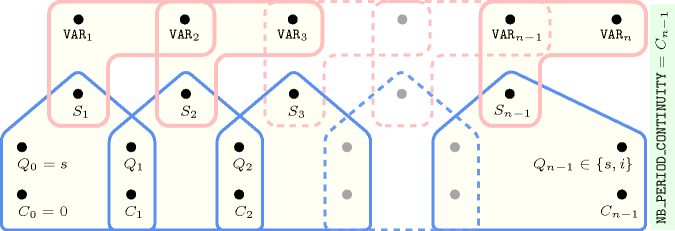
Figure 5.62.7. Automaton for the argument of the constraint; its glue matrix when .
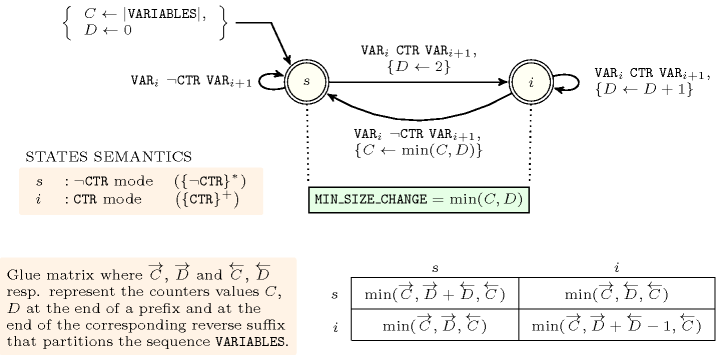
Figure 5.62.8. Automaton for the argument of the constraint; its glue matrix when .
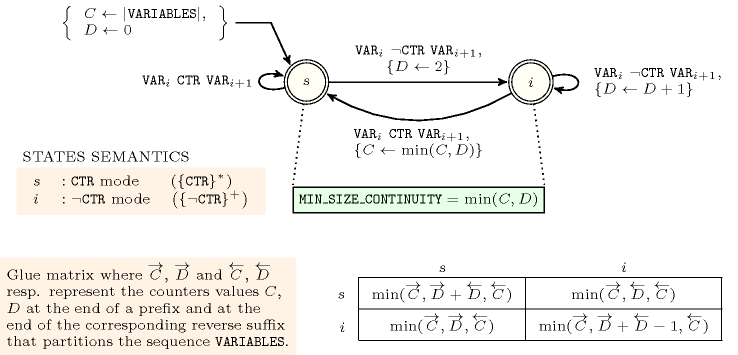
Figure 5.62.9. Hypergraph of the reformulation corresponding to the automaton of the argument of the constraint where stands for (since all states of the automaton are accepting there is no restriction on the last variable )
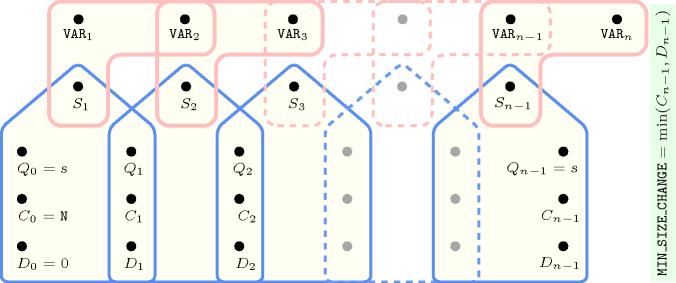
Figure 5.62.10. Hypergraph of the reformulation corresponding to the automaton of the argument of the constraint where stands for (since all states of the automaton are accepting there is no restriction on the last variable )
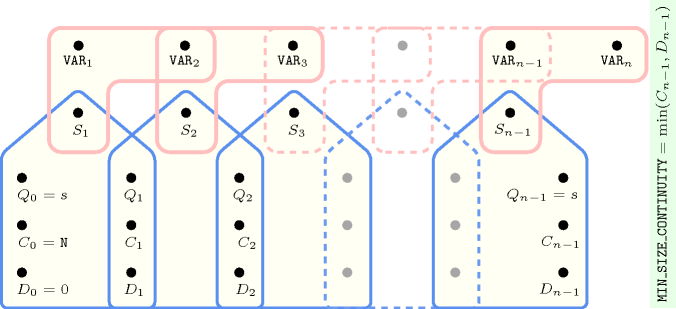
Figure 5.62.11. Automaton for the argument of the constraint; its glue matrix when .
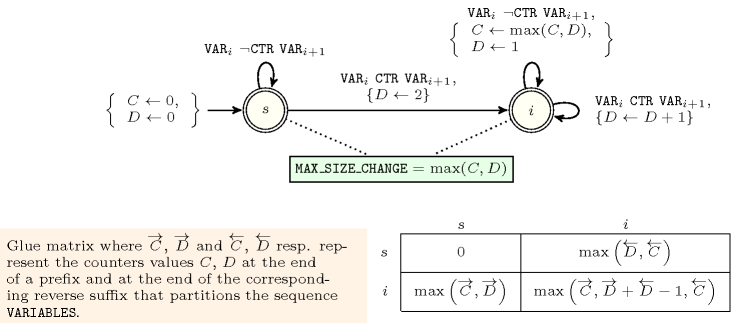
Figure 5.62.12. Automaton for the argument of the constraint; its glue matrix when .
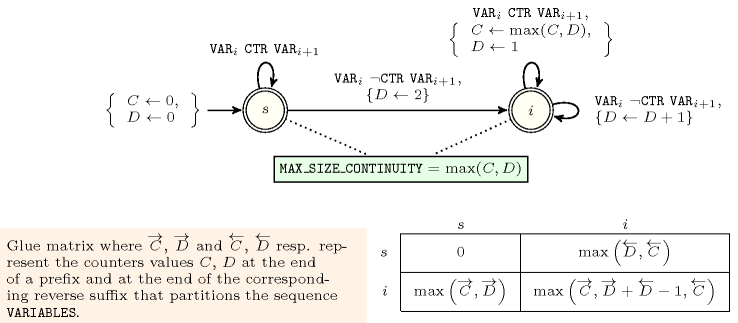
Figure 5.62.13. Hypergraph of the reformulation corresponding to the automaton of the argument of the constraint (since all states of the automaton are accepting there is no restriction on the last variable )
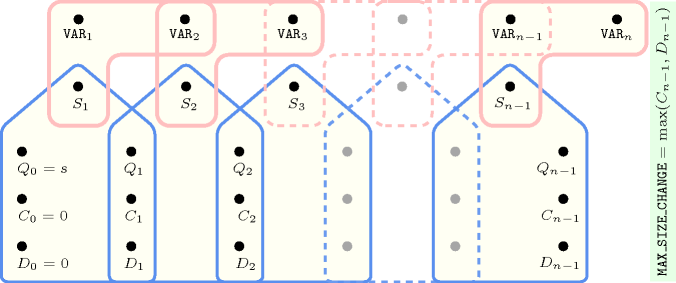
Figure 5.62.14. Hypergraph of the reformulation corresponding to the automaton of the argument of the constraint (since all states of the automaton are accepting there is no restriction on the last variable )
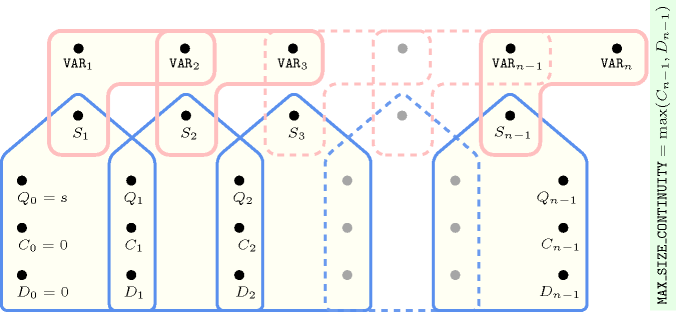
Figure 5.62.15. Automata for the and arguments of the constraint; their common glue matrix when .

Figure 5.62.16. Hypergraph of the reformulation corresponding to the automaton of the argument of the constraint
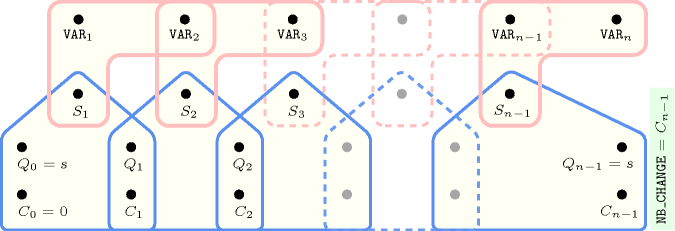
Figure 5.62.17. Hypergraph of the reformulation corresponding to the automaton of the argument of the constraint