Global Constraint Catalog: Cin_interval

5.179. in_interval_reified

DESCRIPTION

LINKS

Origin

Reified version of $𝚒𝚗_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕$ .

Constraint

$𝚒𝚗_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕_𝚛𝚎𝚒𝚏𝚒𝚎𝚍 (𝚅𝙰𝚁, 𝙻𝙾𝚆, 𝚄𝙿, 𝙱)$

Synonyms

$𝚍𝚘𝚖_𝚛𝚎𝚒𝚏𝚒𝚎𝚍$ , $𝚒𝚗_𝚛𝚎𝚒𝚏𝚒𝚎𝚍$ .

Arguments

$𝚅𝙰𝚁$	$𝚍𝚟𝚊𝚛$
$𝙻𝙾𝚆$	$𝚒𝚗𝚝$
$𝚄𝙿$	$𝚒𝚗𝚝$
$𝙱$	$𝚍𝚟𝚊𝚛$

Restrictions

𝙻𝙾𝚆 \leq 𝚄𝙿

𝙱 \geq 0

𝙱 \leq 1

Purpose

Enforce the following equivalence, $𝚅𝙰𝚁 \in [𝙻𝙾𝚆, 𝚄𝙿] \Leftrightarrow 𝙱$ .

Example

(3, 2, 5, 1)

The $𝚒𝚗_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕_𝚛𝚎𝚒𝚏𝚒𝚎𝚍$ constraint holds since:

Its first argument $𝚅𝙰𝚁 = 3$ is greater than or equal to its second argument $𝙻𝙾𝚆 = 2$ and less than or equal to its third argument $𝚄𝙿 = 5$ (i.e., $3 \in [2, 5]$ ).
The corresponding Boolean variable $𝙱$ is set to 1 since condition $3 \in [2, 5]$ holds.

Typical

𝚅𝙰𝚁 \neq 𝙻𝙾𝚆

𝚅𝙰𝚁 \neq 𝚄𝙿

𝙻𝙾𝚆 < 𝚄𝙿

Symmetries

An occurrence of a value of $𝚅𝙰𝚁$ that belongs to $[𝙻𝙾𝚆, 𝚄𝙿]$ (resp. does not belong to $[𝙻𝙾𝚆, 𝚄𝙿]$ ) can be replaced by any other value in $[𝙻𝙾𝚆, 𝚄𝙿]$ ) (resp. not in $[𝙻𝙾𝚆, 𝚄𝙿]$ ).
One and the same constant can be added to $𝚅𝙰𝚁$ , $𝙻𝙾𝚆$ and $𝚄𝙿$ .

Reformulation

The $𝚒𝚗_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕_𝚛𝚎𝚒𝚏𝚒𝚎𝚍$ constraint can be reformulated in terms of linear constraints. For convenience, we rename $𝚅𝙰𝚁$ to $x$ , $𝙻𝙾𝚆$ to $l$ , $𝚄𝙿$ to $u$ , and $𝙱$ to $y$ . The constraint is decomposed into the following conjunction of constraints:

\begin{matrix} x \geq l \Leftrightarrow y_{1}, \\ x \leq u \Leftrightarrow y_{2}, \\ y_{1} \land y_{2} \Leftrightarrow y . \end{matrix}

We show how to encode these constraints with linear inequalities. The first constraint, i.e., $x \geq l \Leftrightarrow y_{1}$ is encoded by posting one of the following three constraints:

\{\begin{matrix} a) & if \underset{̲}{x} \geq l : & y_{1} = 1, \\ b) & if \bar{x} < l : & y_{1} = 0, \\ c) & otherwise : & x \geq (l - \underset{̲}{x}) \cdot y_{1} + \underset{̲}{x} \land x \leq (\bar{x} - l + 1) \cdot y_{1} + l - 1 . \end{matrix}

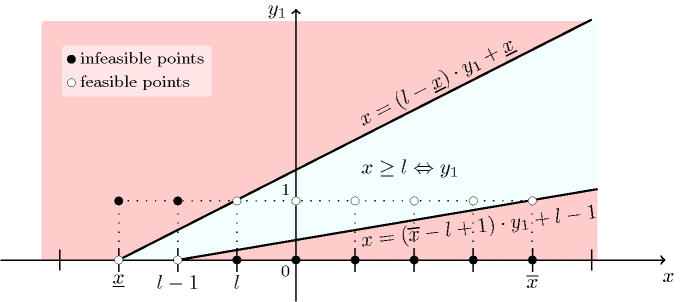
On the one hand, cases a) and b) correspond to situations where one can fix $y_{1}$ , no matter what value will be assigned to $x$ . On the other hand, in case c), $y_{1}$ can take both values 0 or 1 depending on the value assigned to $x$ . As shown by Figure 5.179.1, all possible solutions for the pair of variables $(x, y_{1})$ satisfy the following two linear inequalities $x \geq (l - \underset{̲}{x}) \cdot y_{1} + \underset{̲}{x}$ and $x \leq (\bar{x} - l + 1) \cdot y_{1} + l - 1$ . The first inequality discards all points that are above the line that goes through the two extreme solution points $(\underset{̲}{x}, 0)$ and $(l, 1)$ , while the second one removes all points that are below the line that goes through the two extreme solution points $(l - 1, 0)$ and $(\bar{x}, 1)$ .

Figure 5.179.1. Illustration of the reformulation of the reified constraint $x \geq l \Leftrightarrow y_{1}$ with two linear inequalities

The second constraint, i.e., $x \leq u \Leftrightarrow y_{2}$ is encoded by posting one of the following three constraints:

\{\begin{matrix} d) & if \bar{x} \leq u : & y_{2} = 1, \\ e) & if \underset{̲}{x} > u : & y_{2} = 0, \\ f) & otherwise : & x \leq (u - \bar{x}) \cdot y_{2} + \bar{x} \land x \geq (\underset{̲}{x} - u - 1) \cdot y_{2} + u + 1 . \end{matrix}

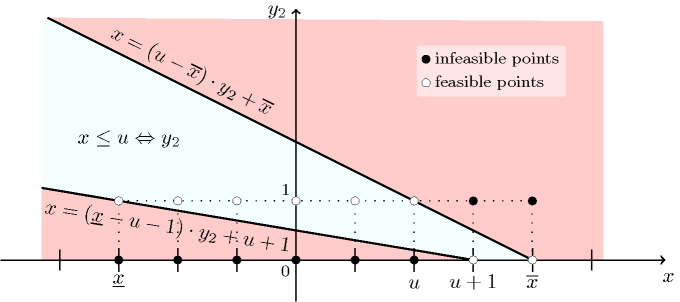
On the one hand, cases d) and e) correspond to situations where one can fix $y_{2}$ , no matter what value will be assigned to $x$ . On the other hand, in case f), $y_{2}$ can take both value 0 or 1 depending on the value assigned to $x$ . As shown by Figure 5.179.2, all possible solutions for the pair of variables $(x, y_{2})$ satisfy the following two linear inequalities $x \leq (u - \bar{x}) \cdot y_{2} + \bar{x}$ and $x \geq (\underset{̲}{x} - u - 1) \cdot y_{2} + u + 1$ . The first inequality discards all points that are above the line that goes through the two extreme solution points $(\bar{x}, 0)$ and $(u, 1)$ , while the second one removes all points that are below the line that goes through the two extreme solution points $(u + 1, 0)$ and $(\underset{̲}{x}, 1)$ .

Figure 5.179.2. Illustration of the reformulation of the reified constraint $x \leq u \Leftrightarrow y_{2}$ with two linear inequalities

The third constraint, i.e., $y_{1} \land y_{2} \Leftrightarrow y$ is encoded as:

\{\begin{matrix} g) & y \geq y_{1} + y_{2} - 1, \\ h) & y \leq y_{1}, \\ i) & y \leq y_{2} . \end{matrix}

Case g) handles the implication $y_{1} \land y_{2} \Rightarrow y$ , while cases h) and i) take care of the other side $y \Rightarrow y_{1} \land y_{2}$ .

See also

specialisation: $𝚒𝚗_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕$ .

uses in its reformulation: $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝$ (bound consistency preserving reformulation).

Keywords

characteristic of a constraint: reified constraint.

constraint arguments: binary constraint.

constraint type: predefined constraint, value constraint.

filtering: arc-consistency.

Global Constraint Catalog

5. Global Constraint Catalogue

5.179. in_interval_reified

Figure 5.179.1. Illustration of the reformulation of the reified constraint x≥l⇔y 1 with two linear inequalities

Figure 5.179.2. Illustration of the reformulation of the reified constraint x≤u⇔y 2 with two linear inequalities

Figure 5.179.1. Illustration of the reformulation of the reified constraint $x \geq l \Leftrightarrow y_{1}$ with two linear inequalities

Figure 5.179.2. Illustration of the reformulation of the reified constraint $x \leq u \Leftrightarrow y_{2}$ with two linear inequalities