Global Constraint Catalog: Cmax

5.243. max_n

DESCRIPTION

LINKS

GRAPH

Origin

[Beldiceanu01]

Constraint

$𝚖𝚊𝚡_𝚗 (𝙼𝙰𝚇, 𝚁𝙰𝙽𝙺, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

Arguments

$𝙼𝙰𝚇$	$𝚍𝚟𝚊𝚛$
$𝚁𝙰𝙽𝙺$	$𝚒𝚗𝚝$
$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)$

Restrictions

𝚁𝙰𝙽𝙺 \geq 0

𝚁𝙰𝙽𝙺 < | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | > 0

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚟𝚊𝚛)

Purpose

$𝙼𝙰𝚇$ is the maximum value of rank $𝚁𝙰𝙽𝙺$ (i.e., the ${𝚁𝙰𝙽𝙺}^{t h}$ largest distinct value, identical values are merged) of the collection of domain variables $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ . The maximum value has rank 0.

Example

(6, 1, 〈3, 1, 7, 1, 6〉)

The $𝚖𝚊𝚡_𝚗$ constraint holds since its first argument $𝙼𝙰𝚇 = 6$ is fixed to the second (i.e., $𝚁𝙰𝙽𝙺 + 1$ ) largest distinct value of the collection $〈 3, 1, 7, 1, 6 〉$ .

Typical

𝚁𝙰𝙽𝙺 > 0

𝚁𝙰𝙽𝙺 < 3

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | > 1

𝚛𝚊𝚗𝚐𝚎

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) > 1

Symmetries

Items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ are permutable.
One and the same constant can be added to $𝙼𝙰𝚇$ as well as to the $𝚟𝚊𝚛$ attribute of all items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ .

Arg. properties

Functional dependency: $𝙼𝙰𝚇$ determined by $𝚁𝙰𝙽𝙺$ and $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ .

Algorithm

[Beldiceanu01].

Reformulation

The constraint $𝚊𝚖𝚘𝚗𝚐_𝚟𝚊𝚛$ $(1, 〈 𝙼𝙰𝚇 〉, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ enforces $𝙼𝙰𝚇$ to be assigned one of the values of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ . The constraint $𝚗𝚟𝚊𝚕𝚞𝚎$ $(𝙽𝚅𝙰𝙻, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ provides a hand on the number of distinct values assigned to the variables of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ . By associating to each variable $V_{i}$ $(i \in [1, | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |])$ of the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ collection a rank variable $R_{i} \in [0, | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | - 1]$ with the reified constraint $R_{i} = 𝚁𝙰𝙽𝙺 \Leftrightarrow V_{i} = 𝙼𝙰𝚇$ , the inequality $R_{i} < 𝙽𝚅𝙰𝙻$ , and by creating for each pair of variables $V_{i}, V_{j}$ $(i, j < i \in [1, | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |])$ the reified constraints

$V_{i} > V_{j} \Leftrightarrow R_{i} < R_{j}$ ,

$V_{i} = V_{j} \Leftrightarrow R_{i} = R_{j}$ ,

$V_{i} < V_{j} \Leftrightarrow R_{i} > R_{j}$ ,

one can reformulate the $𝚖𝚊𝚡_𝚗$ constraint in term of $3 \cdot \frac{| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | \cdot (| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | - 1)}{2} + 1$ reified constraints.

See also

comparison swapped: $𝚖𝚒𝚗_𝚗$ .

generalisation: $𝚖𝚊𝚡𝚒𝚖𝚞𝚖$ (absolute maximum replaced by maximum or order $𝚗$ ).

Keywords

characteristic of a constraint: rank, maximum.

constraint arguments: pure functional dependency.

constraint type: order constraint.

modelling: functional dependency.

Arc input(s)

$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$

Arc generator

𝐶𝐿𝐼𝑄𝑈𝐸

\mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1, 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2)

Arc arity

Arc constraint(s)

⋁ (\begin{matrix} 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1 . 𝚔𝚎𝚢 = 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2 . 𝚔𝚎𝚢, \\ 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1 . 𝚟𝚊𝚛 > 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2 . 𝚟𝚊𝚛 \end{matrix})

Graph property(ies)

𝐎𝐑𝐃𝐄𝐑

(𝚁𝙰𝙽𝙺, 𝙼𝙸𝙽𝙸𝙽𝚃, 𝚟𝚊𝚛) = 𝙼𝙰𝚇

Graph model

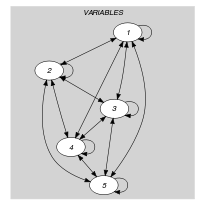
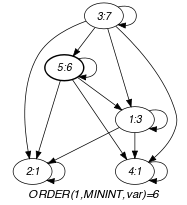
Parts (A) and (B) of Figure 5.243.1 respectively show the initial and final graph associated with the Example slot. Since we use the $𝐎𝐑𝐃𝐄𝐑$ graph property, the vertex of rank 1 (without considering the loops) of the final graph is outlined with a thick circle.

Figure 5.243.1. Initial and final graph of the $𝚖𝚊𝚡_𝚗$ constraint


(a)	(b)

Global Constraint Catalog

5. Global Constraint Catalogue

5.243. max_n

Figure 5.243.1. Initial and final graph of the 𝚖𝚊𝚡_𝚗 constraint

Figure 5.243.1. Initial and final graph of the $𝚖𝚊𝚡_𝚗$ constraint