5.404. tree_range
| DESCRIPTION | LINKS | GRAPH |
- Origin
- Constraint
- Arguments
- Restrictions
- Purpose
Cover the digraph described by the collection with trees in such a way that each vertex of belongs to one distinct tree. is the difference between the longest and the shortest paths (from a leaf to a root) of the final graph.
- Example
-
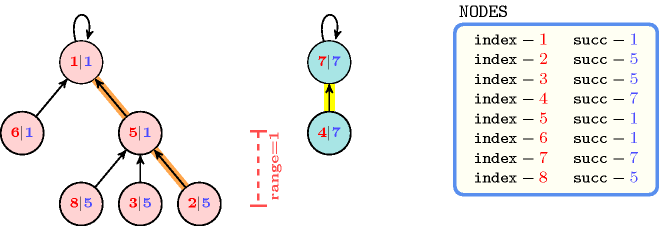
The constraint holds since the graph associated with the items of the collection corresponds to two trees (i.e., ): each tree respectively involves the vertices and . Furthermore is set to the difference between the longest path (for instance ) and the shortest path (for instance ) from a leaf to a root. Figure 5.404.1 provides the two trees associated with the example.
Figure 5.404.1. The two trees corresponding to the Example slot; each vertex contains the information where is the index of its father in the tree (by convention the father of the root is the root itself); the longest and shortest paths from a leaf to a root are respectively shown by thick orange and yellow line segments and have a length of 2 and 1; consequently the range is equal to 1.
- Typical
- Symmetry
Items of are permutable.
- Arg. properties
Functional dependency: determined by .
Functional dependency: determined by .
- Reformulation
By introducing a distance variable , an occurrence variable and a leave variable for each item of the collection, where:
represents the number of vertices from to the root of the corresponding tree,
gives the number of occurrences of value within variables ,
is set to 1 if item corresponds to a leave (i.e., ) and 0 otherwise,
the constraint can be expressed in term of a conjunction of one constraint, constraints, linear constraints, one constraint, reified constraints, one , one and one linear constraint, where:
The constraint models the fact that we have a forest of trees.
Each constraint provides the link between the attribute of the -th item and the distance variable associated with item .
Each linear constraint associated with the -th item states that the difference between the distance variable and the distance variable is equal to 1.
The constraint provides the number of occurrences of value within variables . Note that, when is equal to 0, the corresponding -th item is a leave of one of the trees.
Each reified constraint of the form makes the link between the -th occurrence variable and the -th leave variable .
The constraint computes the minimum distance from the leaves to the corresponding roots. The leave variable is used in order to select only the distance variables corresponding to leaves.
The constraint computes the maximum distance from the vertices to the roots. Since the maximum is achieved by a leave we do not need to focus just on the leaves as it was the case for the minimum distance .
The linear constraint links together argument to the minimum and maximum distances.
With respect to the Example slot we get the following conjunction of constraints:
,
,
,
,
.
- See also
related: (balanced tree versus balanced assignment).
used in reformulation: , , , , , .
- Keywords
constraint type: graph constraint, graph partitioning constraint.
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
- Graph property(ies)
-
- Graph model
Parts (A) and (B) of Figure 5.404.2 respectively show the initial and final graph associated with the Example slot. Since we use the graph property, we respectively display the longest and shortest paths of the final graph with a bold and a dash line.
Figure 5.404.2. Initial and final graph of the constraint
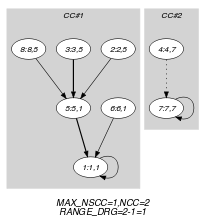
(a) (b)