Global Constraint Catalog: Cused_by

5.414. used_by_modulo

DESCRIPTION

LINKS

GRAPH

Origin

Derived from $𝚞𝚜𝚎𝚍_𝚋𝚢$ .

Constraint

$𝚞𝚜𝚎𝚍_𝚋𝚢_𝚖𝚘𝚍𝚞𝚕𝚘 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2, 𝙼)$

Arguments

$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)$
$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)$
$𝙼$	$𝚒𝚗𝚝$

Restrictions

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 | \geq | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 |

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1, 𝚟𝚊𝚛)

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2, 𝚟𝚊𝚛)

𝙼 > 0

Purpose

For each integer $R$ in $[0, 𝙼 - 1]$ , let $𝑁 1_{R}$ (respectively $𝑁 2_{R}$ ) denote the number of variables of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ (respectively $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ ) that have $R$ as a rest when divided by $𝙼$ . For all $R$ in $[0, 𝙼 - 1]$ we have $𝑁 2_{R} > 0 \Rightarrow 𝑁 1_{R} \geq 𝑁 2_{R}$ .

Example

(〈1, 9, 4, 5, 2, 1〉, 〈7, 1, 2, 5〉, 3)

The values of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 = 〈 7, 1, 2, 5 〉$ are respectively associated with the equivalence classes $7 \mod 3 = 1$ , $1 \mod 3 = 1$ , $2 \mod 3 = 2$ , $5 \mod 3 = 2$ . Therefore the equivalence classes 1 and 2 are respectively used 2 and 2 times.

Similarly, the values of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 = 〈 1, 9, 4, 5, 2, 1 〉$ associated with the equivalence classes $1 \mod 3 = 1$ , $9 \mod 3 = 0$ , $4 \mod 3 = 1$ , $5 \mod 3 = 2$ , $2 \mod 3 = 2$ , $1 \mod 3 = 1$ . Therefore the equivalence classes 0, 1 and 2 are respectively used 1, 3 and 2 times.

Consequently, the $𝚞𝚜𝚎𝚍_𝚋𝚢_𝚖𝚘𝚍𝚞𝚕𝚘$ constraint holds since, for each equivalence class associated with the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 = 〈 7, 1, 2, 5 〉$ , its number of occurrences within $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 = 〈 1, 9, 4, 5, 2, 1 〉$ is greater than or equal to its number of occurrences within $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ :

The equivalence class 1 occurs 3 times within $〈 1, 9, 4, 5, 2, 1 〉$ and 2 times within $〈 7, 1, 2, 5 〉$ .
The equivalence class 2 occurs 2 times within $〈 1, 9, 4, 5, 2, 1 〉$ and 2 times within $〈 7, 1, 2, 5 〉$ .

Typical

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 | > 1

𝚛𝚊𝚗𝚐𝚎

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 . 𝚟𝚊𝚛) > 1

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 | > 1

𝚛𝚊𝚗𝚐𝚎

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 . 𝚟𝚊𝚛) > 1

𝙼 > 1

𝙼 <

𝚖𝚊𝚡𝚟𝚊𝚕

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 . 𝚟𝚊𝚛)

𝙼 <

𝚖𝚊𝚡𝚟𝚊𝚕

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 . 𝚟𝚊𝚛)

Symmetries

Items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ are permutable.
Items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ are permutable.
An occurrence of a value $u$ of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 . 𝚟𝚊𝚛$ can be replaced by any other value $v$ such that $v$ is congruent to $u$ modulo $𝙼$ .
An occurrence of a value $u$ of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 . 𝚟𝚊𝚛$ can be replaced by any other value $v$ such that $v$ is congruent to $u$ modulo $𝙼$ .

Arg. properties

Contractible wrt. $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ .
Extensible wrt. $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ .
Aggregate: $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 (𝚞𝚗𝚒𝚘𝚗)$ , $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 (𝚞𝚗𝚒𝚘𝚗)$ , $𝙼 (𝚒𝚍)$ .

Used in

$𝚔_𝚞𝚜𝚎𝚍_𝚋𝚢_𝚖𝚘𝚍𝚞𝚕𝚘$ .

See also

implied by: $𝚜𝚊𝚖𝚎_𝚖𝚘𝚍𝚞𝚕𝚘$ .

soft variant: $𝚜𝚘𝚏𝚝_𝚞𝚜𝚎𝚍_𝚋𝚢_𝚖𝚘𝚍𝚞𝚕𝚘_𝚟𝚊𝚛$ (variable-based violation measure).

specialisation: $𝚞𝚜𝚎𝚍_𝚋𝚢$ ( $𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎 \mod 𝚌𝚘𝚗𝚜𝚝𝚊𝚗𝚝$ replaced by $𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎$ ).

system of constraints: $𝚔_𝚞𝚜𝚎𝚍_𝚋𝚢_𝚖𝚘𝚍𝚞𝚕𝚘$ .

Keywords

characteristic of a constraint: modulo, sort based reformulation.

constraint arguments: constraint between two collections of variables.

modelling: inclusion.

Arc input(s)

$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$

Arc generator

𝑃𝑅𝑂𝐷𝑈𝐶𝑇

\mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1, 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2)

Arc arity

Arc constraint(s)

𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1 . 𝚟𝚊𝚛 \mod 𝙼 = 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2 . 𝚟𝚊𝚛 \mod 𝙼

Graph property(ies)

• for all connected components:

𝐍𝐒𝐎𝐔𝐑𝐂𝐄

\geq

𝐍𝐒𝐈𝐍𝐊

•

𝐍𝐒𝐈𝐍𝐊

= | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 |

Graph model

Parts (A) and (B) of Figure 5.414.1 respectively show the initial and final graph associated with the Example slot. Since we use the $𝐍𝐒𝐎𝐔𝐑𝐂𝐄$ and $𝐍𝐒𝐈𝐍𝐊$ graph properties, the source and sink vertices of the final graph are stressed with a double circle. Since there is a constraint on each connected component of the final graph we also show the different connected components. Each of them corresponds to an equivalence class according to the arc constraint. Note that the vertex corresponding to the variable that takes value 9 was removed from the final graph since there is no arc for which the associated equivalence constraint holds. The $𝚞𝚜𝚎𝚍_𝚋𝚢_𝚖𝚘𝚍𝚞𝚕𝚘$ constraint holds since:

For each connected component of the final graph the number of sources is greater than or equal to the number of sinks.
The number of sinks of the final graph is equal to $| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 |$ .

Figure 5.414.1. Initial and final graph of the $𝚞𝚜𝚎𝚍_𝚋𝚢_𝚖𝚘𝚍𝚞𝚕𝚘$ constraint

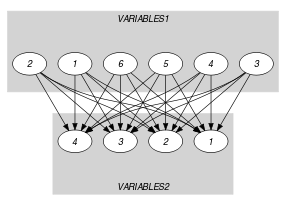
(a)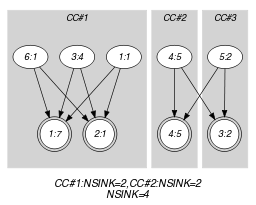

(b)

Signature

Since the initial graph contains only sources and sinks, and since sources of the initial graph cannot become sinks of the final graph, we have that the maximum number of sinks of the final graph is equal to $| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 |$ . Therefore we can rewrite $𝐍𝐒𝐈𝐍𝐊 = | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 |$ to $𝐍𝐒𝐈𝐍𝐊 \geq | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 |$ and simplify $\underset{̲}{\bar{𝐍𝐒𝐈𝐍𝐊}}$ to $\bar{𝐍𝐒𝐈𝐍𝐊}$ .

Global Constraint Catalog

5. Global Constraint Catalogue

5.414. used_by_modulo

Figure 5.414.1. Initial and final graph of the 𝚞𝚜𝚎𝚍_𝚋𝚢_𝚖𝚘𝚍𝚞𝚕𝚘 constraint

Figure 5.414.1. Initial and final graph of the $𝚞𝚜𝚎𝚍_𝚋𝚢_𝚖𝚘𝚍𝚞𝚕𝚘$ constraint