Global Constraint Catalog: Csliding_time

5.352. sliding_time_window

DESCRIPTION

LINKS

GRAPH

Origin

N. Beldiceanu

Constraint

$𝚜𝚕𝚒𝚍𝚒𝚗𝚐_𝚝𝚒𝚖𝚎_𝚠𝚒𝚗𝚍𝚘𝚠 (𝚆𝙸𝙽𝙳𝙾𝚆_𝚂𝙸𝚉𝙴, 𝙻𝙸𝙼𝙸𝚃, 𝚃𝙰𝚂𝙺𝚂)$

Arguments

$𝚆𝙸𝙽𝙳𝙾𝚆_𝚂𝙸𝚉𝙴$	$𝚒𝚗𝚝$
$𝙻𝙸𝙼𝙸𝚃$	$𝚒𝚗𝚝$
$𝚃𝙰𝚂𝙺𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚘𝚛𝚒𝚐𝚒𝚗 - 𝚍𝚟𝚊𝚛, 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 - 𝚍𝚟𝚊𝚛)$

Restrictions

𝚆𝙸𝙽𝙳𝙾𝚆_𝚂𝙸𝚉𝙴 > 0

𝙻𝙸𝙼𝙸𝚃 \geq 0

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚃𝙰𝚂𝙺𝚂, [𝚘𝚛𝚒𝚐𝚒𝚗, 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗])

𝚃𝙰𝚂𝙺𝚂 . 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 \geq 0

Purpose

For any time window of size $𝚆𝙸𝙽𝙳𝙾𝚆_𝚂𝙸𝚉𝙴$ , the intersection of all the tasks of the collection $𝚃𝙰𝚂𝙺𝚂$ with this time window is less than or equal to a given limit $𝙻𝙸𝙼𝙸𝚃$ .

Example

(\begin{matrix} 9, 6, 〈\begin{matrix} 𝚘𝚛𝚒𝚐𝚒𝚗 - 10 & 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 - 3, \\ 𝚘𝚛𝚒𝚐𝚒𝚗 - 5 & 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 - 1, \\ 𝚘𝚛𝚒𝚐𝚒𝚗 - 6 & 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 - 2, \\ 𝚘𝚛𝚒𝚐𝚒𝚗 - 14 & 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 - 2, \\ 𝚘𝚛𝚒𝚐𝚒𝚗 - 2 & 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 - 2 \end{matrix}〉 \end{matrix})

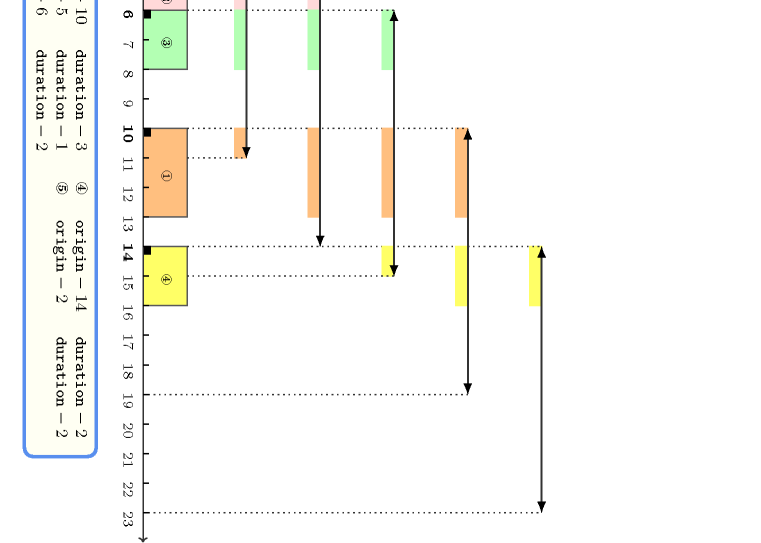
The lower part of Figure 5.352.1 indicates the different tasks on the time axis. Each task is drawn as a rectangle with its corresponding identifier in the middle. Finally the upper part of Figure 5.352.1 shows the different time windows and the respective contribution of the tasks in these time windows. Note that we only need to focus on those time windows starting at the start of one of the tasks. A line with two arrows depicts each time window. The two arrows indicate the start and the end of the time window. At the left of each time window we give its occupation. Since this occupation is always less than or equal to the limit 6, the $𝚜𝚕𝚒𝚍𝚒𝚗𝚐_𝚝𝚒𝚖𝚎_𝚠𝚒𝚗𝚍𝚘𝚠$ constraint holds.

Figure 5.352.1. Time windows and their use for the five tasks of the Example slot

Typical

𝚆𝙸𝙽𝙳𝙾𝚆_𝚂𝙸𝚉𝙴 > 1

𝙻𝙸𝙼𝙸𝚃 > 0

𝙻𝙸𝙼𝙸𝚃 <

𝚜𝚞𝚖

(𝚃𝙰𝚂𝙺𝚂 . 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗)

| 𝚃𝙰𝚂𝙺𝚂 | > 1

𝚃𝙰𝚂𝙺𝚂 . 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 > 0

Symmetries

$𝚆𝙸𝙽𝙳𝙾𝚆_𝚂𝙸𝚉𝙴$ can be decreased.
$𝙻𝙸𝙼𝙸𝚃$ can be increased.
Items of $𝚃𝙰𝚂𝙺𝚂$ are permutable.
One and the same constant can be added to the $𝚘𝚛𝚒𝚐𝚒𝚗$ attribute of all items of $𝚃𝙰𝚂𝙺𝚂$ .
$𝚃𝙰𝚂𝙺𝚂 . 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗$ can be decreased to any value $\geq 0$ .

Arg. properties

Contractible wrt. $𝚃𝙰𝚂𝙺𝚂$ .

Usage

The $𝚜𝚕𝚒𝚍𝚒𝚗𝚐_𝚝𝚒𝚖𝚎_𝚠𝚒𝚗𝚍𝚘𝚠$ constraint is useful for timetabling problems in order to put an upper limit on the total work over sliding time windows.

Reformulation

The $𝚜𝚕𝚒𝚍𝚒𝚗𝚐_𝚝𝚒𝚖𝚎_𝚠𝚒𝚗𝚍𝚘𝚠$ constraint can be expressed in term of a set of ${| 𝚃𝙰𝚂𝙺𝚂 |}^{2}$ reified constraints and of $| 𝚃𝙰𝚂𝙺𝚂 |$ linear inequalities constraints:

For each pair of tasks $𝚃𝙰𝚂𝙺𝚂 [i], 𝚃𝙰𝚂𝙺𝚂 [j]$ $(i, j \in [1, | 𝚃𝙰𝚂𝙺𝚂 |])$ of the $𝚃𝙰𝚂𝙺𝚂$ collection we create a variable ${𝐼𝑛𝑡𝑒𝑟}_{i j}$ which is set to the intersection of $𝚃𝙰𝚂𝙺𝚂 [j]$ with the time window $𝒲_{i}$ of size $𝚆𝙸𝙽𝙳𝙾𝚆_𝚂𝙸𝚉𝙴$ that starts at instant $𝚃𝙰𝚂𝙺𝚂 [i] . 𝚘𝚛𝚒𝚐𝚒𝚗$ :
- If $i = j$ (i.e., $𝚃𝙰𝚂𝙺𝚂 [i]$ and $𝚃𝙰𝚂𝙺𝚂 [j]$ coincide):
  - ${𝐼𝑛𝑡𝑒𝑟}_{i j} = min (𝚃𝙰𝚂𝙺𝚂 [i] . 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗, 𝚆𝙸𝙽𝙳𝙾𝚆_𝚂𝙸𝚉𝙴)$ .
- If $i \neq j$ and $\bar{𝚃𝙰𝚂𝙺𝚂 [j] . 𝚘𝚛𝚒𝚐𝚒𝚗} + \bar{𝚃𝙰𝚂𝙺𝚂 [j] . 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗} < \underset{̲}{𝚃𝙰𝚂𝙺𝚂 [i] . 𝚘𝚛𝚒𝚐𝚒𝚗}$ (i.e., $𝚃𝙰𝚂𝙺𝚂 [j]$ for sure ends before the time window $𝒲_{i}$ ):
  - ${𝐼𝑛𝑡𝑒𝑟}_{i j} = 0$ .
- If $i \neq j$ and $\underset{̲}{𝚃𝙰𝚂𝙺𝚂 [j] . 𝚘𝚛𝚒𝚐𝚒𝚗} > \bar{𝚃𝙰𝚂𝙺𝚂 [i] . 𝚘𝚛𝚒𝚐𝚒𝚗} + 𝚆𝙸𝙽𝙳𝙾𝚆_𝚂𝙸𝚉𝙴 - 1$ (i.e., $𝚃𝙰𝚂𝙺𝚂 [j]$ for sure starts after the time window $𝒲_{i}$ ):
  - ${𝐼𝑛𝑡𝑒𝑟}_{i j} = 0$ .
- Otherwise (i.e., $𝚃𝙰𝚂𝙺𝚂 [j]$ can potentially overlap the time window $𝒲_{i}$ ):
  - ${𝐼𝑛𝑡𝑒𝑟}_{i j} = max (0, min (𝚃𝙰𝚂𝙺𝚂 [i] . 𝚘𝚛𝚒𝚐𝚒𝚗 + 𝚆𝙸𝙽𝙳𝙾𝚆_𝚂𝙸𝚉𝙴, 𝚃𝙰𝚂𝙺𝚂 [j] . 𝚘𝚛𝚒𝚐𝚒𝚗 + 𝚃𝙰𝚂𝙺𝚂 [j] . 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗) - max (𝚃𝙰𝚂𝙺𝚂 [i] . 𝚘𝚛𝚒𝚐𝚒𝚗, 𝚃𝙰𝚂𝙺𝚂 [j] . 𝚘𝚛𝚒𝚐𝚒𝚗))$ .
For each task $𝚃𝙰𝚂𝙺𝚂 [i]$ $(i \in [1, | 𝚃𝙰𝚂𝙺𝚂 |])$ we create a linear inequality constraint ${𝐼𝑛𝑡𝑒𝑟}_{i 1} + {𝐼𝑛𝑡𝑒𝑟}_{i 2} + \dots + {𝐼𝑛𝑡𝑒𝑟}_{i | 𝚃𝙰𝚂𝙺𝚂 |} \leq 𝙻𝙸𝙼𝙸𝚃$ .

related: $𝚜𝚕𝚒𝚍𝚒𝚗𝚐_𝚝𝚒𝚖𝚎_𝚠𝚒𝚗𝚍𝚘𝚠_𝚜𝚞𝚖$ (sum of intersections of tasks with sliding time window replaced by sum of the points of intersecting tasks with sliding time window).

used in graph description: $𝚜𝚕𝚒𝚍𝚒𝚗𝚐_𝚝𝚒𝚖𝚎_𝚠𝚒𝚗𝚍𝚘𝚠_𝚏𝚛𝚘𝚖_𝚜𝚝𝚊𝚛𝚝$ .

Keywords

constraint type: sliding sequence constraint, temporal constraint.

Arc input(s)

$𝚃𝙰𝚂𝙺𝚂$

Arc generator

𝐶𝐿𝐼𝑄𝑈𝐸

\mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚝𝚊𝚜𝚔𝚜 1, 𝚝𝚊𝚜𝚔𝚜 2)

Arc arity

Arc constraint(s)

• 𝚝𝚊𝚜𝚔𝚜 1 . 𝚘𝚛𝚒𝚐𝚒𝚗 \leq 𝚝𝚊𝚜𝚔𝚜 2 . 𝚘𝚛𝚒𝚐𝚒𝚗

• 𝚝𝚊𝚜𝚔𝚜 2 . 𝚘𝚛𝚒𝚐𝚒𝚗 - 𝚝𝚊𝚜𝚔𝚜 1 . 𝚘𝚛𝚒𝚐𝚒𝚗 < 𝚆𝙸𝙽𝙳𝙾𝚆_𝚂𝙸𝚉𝙴

Sets

𝖲𝖴𝖢𝖢 \mapsto [𝚜𝚘𝚞𝚛𝚌𝚎, 𝚝𝚊𝚜𝚔𝚜]

Constraint(s) on sets

𝚜𝚕𝚒𝚍𝚒𝚗𝚐_𝚝𝚒𝚖𝚎_𝚠𝚒𝚗𝚍𝚘𝚠_𝚏𝚛𝚘𝚖_𝚜𝚝𝚊𝚛𝚝

(\begin{matrix} 𝚆𝙸𝙽𝙳𝙾𝚆_𝚂𝙸𝚉𝙴, \\ 𝙻𝙸𝙼𝙸𝚃, \\ 𝚝𝚊𝚜𝚔𝚜, \\ 𝚜𝚘𝚞𝚛𝚌𝚎 . 𝚘𝚛𝚒𝚐𝚒𝚗 \end{matrix})

Graph model

We generate an arc from a task $t_{1}$ to a task $t_{2}$ if task $t_{2}$ does not start before task $t_{1}$ and if task $t_{2}$ intersects the time window that starts at the origin of task $t_{1}$ . Each set generated by $𝖲𝖴𝖢𝖢$ corresponds to all tasks that intersect in time the time window that starts at the origin of a given task.

Parts (A) and (B) of Figure 5.352.2 respectively show the initial and final graph associated with the Example slot. In the final graph, the successors of a given task $t$ correspond to the set of tasks that do not start before task $t$ and intersect the time window that starts at the origin of task $t$ .

Figure 5.352.2. Initial and final graph of the $𝚜𝚕𝚒𝚍𝚒𝚗𝚐_𝚝𝚒𝚖𝚎_𝚠𝚒𝚗𝚍𝚘𝚠$ constraint


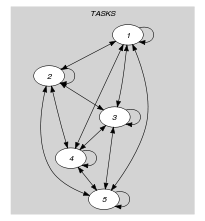
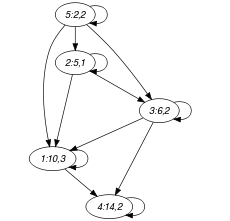
(a)	(b)

Global Constraint Catalog

5. Global Constraint Catalogue

5.352. sliding_time_window

Figure 5.352.1. Time windows and their use for the five tasks of the Example slot

Figure 5.352.2. Initial and final graph of the 𝚜𝚕𝚒𝚍𝚒𝚗𝚐_𝚝𝚒𝚖𝚎_𝚠𝚒𝚗𝚍𝚘𝚠 constraint

Figure 5.352.2. Initial and final graph of the $𝚜𝚕𝚒𝚍𝚒𝚗𝚐_𝚝𝚒𝚖𝚎_𝚠𝚒𝚗𝚍𝚘𝚠$ constraint