5.86. connected
| DESCRIPTION | LINKS | GRAPH |
- Origin
- Constraint
- Argument
- Restrictions
- Purpose
Consider a digraph described by the collection. Select a subset of arcs of so that the corresponding graph is symmetric (i.e., if there is an arc from to , there is also an arc from to ) and connected (i.e., there is a path between any pair of vertices of ).
- Example
-
The constraint holds since the collection depicts a symmetric graph involving a single connected component.
- Typical
- Symmetry
Items of are permutable.
- Algorithm
A filtering algorithm for the constraint is sketched in [Dooms06]. Beside the pruning associated with the fact that the final graph is symmetric, it is based on the fact that all bridges and cut vertices on a path between two vertices that should for sure belong to the final graph should also belong to the final graph.
- See also
-
implies: .
- Keywords
constraint arguments: constraint involving set variables.
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
- Graph property(ies)
-
- Graph class
-
- Graph model
Part (A) of Figure 5.86.1 shows the initial graph from which we start. It is derived from the set associated with each vertex. Each set describes the potential values of the attribute of a given vertex. Part (B) of Figure 5.86.1 gives the final graph associated with the Example slot.
Figure 5.86.1. Initial and final graph of the set constraint
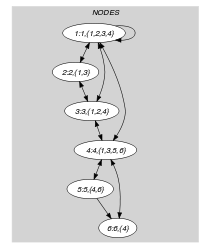
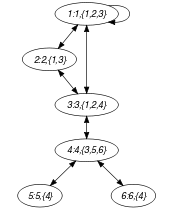
(a) (b)