5.365. soft_same_var
| DESCRIPTION | LINKS | GRAPH |
- Origin
- Constraint
- Synonym
.
- Arguments
- Restrictions
- Purpose
is the minimum number of values to change in the and collections so that the variables of the collection correspond to the variables of the collection according to a permutation.
- Example
-
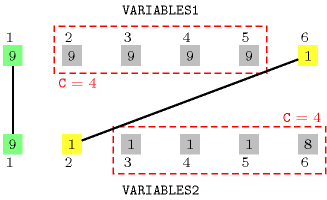
As illustrated by Figure 5.365.1, there is a correspondence between two pairs of values of the collections and . Consequently, we must unset at least items (6 is the number of items of the and collections). The constraint holds since its first argument is set to .
Figure 5.365.1. Illustration of the partial correspondence between the items of the and of the collections of the Example slot, i.e., items of the or of the collections need to be changed in order to have a full correspondence
- Typical
- Symmetries
Arguments are permutable w.r.t. permutation .
Items of are permutable.
Items of are permutable.
All occurrences of two distinct values in or can be swapped; all occurrences of a value in or can be renamed to any unused value.
- Usage
- Algorithm
A first filtering algorithm is described in [vanHoeve05]. A second filtering algorithm is presented in [Cymer12], [CymerPhD13].
- See also
-
implies: .
- Keywords
constraint arguments: constraint between two collections of variables.
constraint type: soft constraint, relaxation, variable-based violation measure.
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
- Graph property(ies)
-
- Graph model
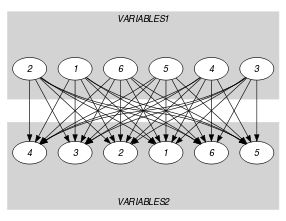
Parts (A) and (B) of Figure 5.365.2 respectively show the initial and final graph associated with the Example slot. Since we use the graph property, the source and sink vertices of the final graph are stressed with a double circle. The constraint holds since the cost 4 corresponds to the difference between the number of variables of and the sum over the different connected components of the minimum number of sources and sinks.
Figure 5.365.2. Initial and final graph of the constraint
(a) 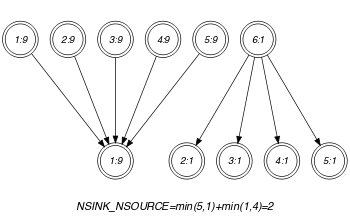
(b)