Global Constraint Catalog: Cpermutation

5.322. permutation

DESCRIPTION

LINKS

GRAPH

Origin

Derived from $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚌𝚘𝚗𝚜𝚎𝚌𝚞𝚝𝚒𝚟𝚎_𝚟𝚊𝚕𝚞𝚎𝚜$ .

Constraint

$𝚙𝚎𝚛𝚖𝚞𝚝𝚊𝚝𝚒𝚘𝚗 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

Argument

𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂

𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)

Restrictions

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚟𝚊𝚛)

𝚖𝚒𝚗𝚟𝚊𝚕

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) = 1

𝚖𝚊𝚡𝚟𝚊𝚕

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) = | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |

Purpose

Enforce all variables of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ to take distinct values between 1 and the total number of variables.

Example

(〈3, 2, 1, 4〉)

The $𝚙𝚎𝚛𝚖𝚞𝚝𝚊𝚝𝚒𝚘𝚗$ constraint holds since all the values 3, 2, 1 and 4 are distinct, and since they all belong to interval $[1, 4]$ where 4 is the total number of variables.

Typical

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | > 2

Symmetries

Items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ are permutable.
Two distinct values of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛$ can be swapped.

Usage

See Usage slot of $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝$ .

Algorithm

See Algorithm slot of $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝$ .

Counting

Length ( $n$ )	2	3	4	5	6	7	8	9	10
Solutions	2	6	24	120	720	5040	40320	362880	3628800

Number of solutions for $𝚙𝚎𝚛𝚖𝚞𝚝𝚊𝚝𝚒𝚘𝚗$ : domains $0 . . n$

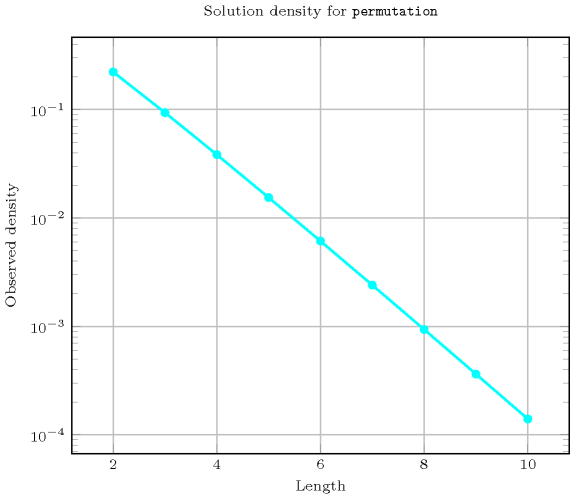
ctrs/permutation-1-tikz

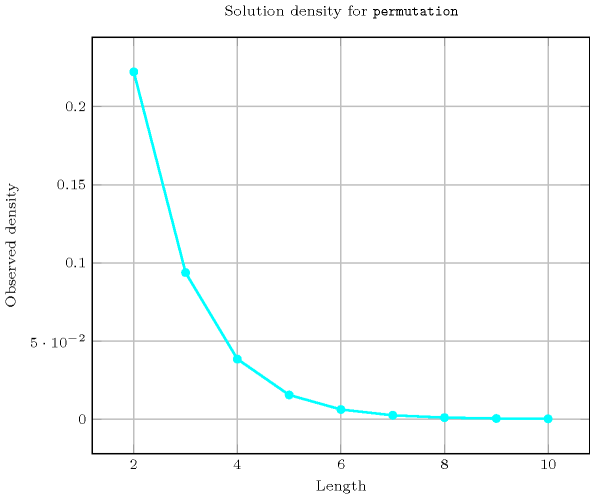
ctrs/permutation-2-tikz

See also

implied by: $𝚙𝚛𝚘𝚙𝚎𝚛_𝚌𝚒𝚛𝚌𝚞𝚒𝚝$ .

implies: $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚌𝚘𝚗𝚜𝚎𝚌𝚞𝚝𝚒𝚟𝚎_𝚟𝚊𝚕𝚞𝚎𝚜$ .

Keywords

characteristic of a constraint: all different, disequality, sort based reformulation.

combinatorial object: permutation.

constraint type: value constraint.

final graph structure: one_succ.

Cond. implications

$•$ $𝚙𝚎𝚛𝚖𝚞𝚝𝚊𝚝𝚒𝚘𝚗 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

implies $𝚋𝚊𝚕𝚊𝚗𝚌𝚎$ $(𝙱𝙰𝙻𝙰𝙽𝙲𝙴, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

when $𝙱𝙰𝙻𝙰𝙽𝙲𝙴 = 0$ .

$•$ $𝚙𝚎𝚛𝚖𝚞𝚝𝚊𝚝𝚒𝚘𝚗 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

implies $𝚌𝚑𝚊𝚗𝚐𝚎$ $(𝙽𝙲𝙷𝙰𝙽𝙶𝙴, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝙲𝚃𝚁)$

when $𝙽𝙲𝙷𝙰𝙽𝙶𝙴 = | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | - 1$

and $𝙲𝚃𝚁 \in [\neq]$ .

$•$ $𝚙𝚎𝚛𝚖𝚞𝚝𝚊𝚝𝚒𝚘𝚗 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

implies $𝚌𝚒𝚛𝚌𝚞𝚕𝚊𝚛_𝚌𝚑𝚊𝚗𝚐𝚎$ $(𝙽𝙲𝙷𝙰𝙽𝙶𝙴, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝙲𝚃𝚁)$

when $𝙽𝙲𝙷𝙰𝙽𝙶𝙴 = | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |$

and $𝙲𝚃𝚁 \in [\neq]$ .

$•$ $𝚙𝚎𝚛𝚖𝚞𝚝𝚊𝚝𝚒𝚘𝚗 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

implies $𝚕𝚎𝚗𝚐𝚝𝚑_𝚕𝚊𝚜𝚝_𝚜𝚎𝚚𝚞𝚎𝚗𝚌𝚎$ $(𝙻𝙴𝙽, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

when $𝙻𝙴𝙽 = 1$ .

$•$ $𝚙𝚎𝚛𝚖𝚞𝚝𝚊𝚝𝚒𝚘𝚗 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

implies $𝚕𝚎𝚗𝚐𝚝𝚑_𝚏𝚒𝚛𝚜𝚝_𝚜𝚎𝚚𝚞𝚎𝚗𝚌𝚎$ $(𝙻𝙴𝙽, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

when $𝙻𝙴𝙽 = 1$ .

$•$ $𝚙𝚎𝚛𝚖𝚞𝚝𝚊𝚝𝚒𝚘𝚗 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

implies $𝚕𝚘𝚗𝚐𝚎𝚜𝚝_𝚌𝚑𝚊𝚗𝚐𝚎$ $(𝚂𝙸𝚉𝙴, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝙲𝚃𝚁)$

when $𝚂𝙸𝚉𝙴 = | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |$

and $𝙲𝚃𝚁 \in [\neq]$ .

$•$ $𝚙𝚎𝚛𝚖𝚞𝚝𝚊𝚝𝚒𝚘𝚗 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

implies $𝚖𝚊𝚡_𝚗$ $(𝙼𝙰𝚇, 𝚁𝙰𝙽𝙺, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

when $𝙼𝙰𝚇 = | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | - 𝚁𝙰𝙽𝙺$ .

$•$ $𝚙𝚎𝚛𝚖𝚞𝚝𝚊𝚝𝚒𝚘𝚗 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

implies $𝚖𝚒𝚗_𝚗$ $(𝙼𝙸𝙽, 𝚁𝙰𝙽𝙺, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

when $𝙼𝙸𝙽 = 𝚁𝙰𝙽𝙺 + 1$ .

$•$ $𝚙𝚎𝚛𝚖𝚞𝚝𝚊𝚝𝚒𝚘𝚗 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

implies $𝚖𝚒𝚗_𝚗𝚟𝚊𝚕𝚞𝚎$ $(𝙼𝙸𝙽, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

when $𝙼𝙸𝙽 = 1$ .

$•$ $𝚙𝚎𝚛𝚖𝚞𝚝𝚊𝚝𝚒𝚘𝚗 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

implies $𝚖𝚒𝚗_𝚜𝚒𝚣𝚎_𝚏𝚞𝚕𝚕_𝚣𝚎𝚛𝚘_𝚜𝚝𝚛𝚎𝚝𝚌𝚑$ $(𝙼𝙸𝙽𝚂𝙸𝚉𝙴, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

when $𝙼𝙸𝙽𝚂𝙸𝚉𝙴 = | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |$ .

$•$ $𝚙𝚎𝚛𝚖𝚞𝚝𝚊𝚝𝚒𝚘𝚗 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

implies $𝚗𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕$ $(𝙽𝚅𝙰𝙻, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻)$

when $𝙽𝚅𝙰𝙻 = (| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | + 𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻) / 𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻$ .

$•$ $𝚙𝚎𝚛𝚖𝚞𝚝𝚊𝚝𝚒𝚘𝚗 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

implies $𝚛𝚊𝚗𝚐𝚎_𝚌𝚝𝚛$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝙲𝚃𝚁, 𝚁)$

when $𝙲𝚃𝚁 \in [\leq]$

and $𝚁 = | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |$ .

$•$ $𝚙𝚎𝚛𝚖𝚞𝚝𝚊𝚝𝚒𝚘𝚗 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

implies $𝚜𝚘𝚏𝚝_𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚌𝚝𝚛$ $(𝙲, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ .

$•$ $𝚙𝚎𝚛𝚖𝚞𝚝𝚊𝚝𝚒𝚘𝚗 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

implies $𝚜𝚘𝚏𝚝_𝚊𝚕𝚕_𝚎𝚚𝚞𝚊𝚕_𝚖𝚊𝚡_𝚟𝚊𝚛$ $(𝙽, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

when $𝙽 \leq | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | - 1$ .

$•$ $𝚙𝚎𝚛𝚖𝚞𝚝𝚊𝚝𝚒𝚘𝚗 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

implies $𝚜𝚘𝚏𝚝_𝚊𝚕𝚕_𝚎𝚚𝚞𝚊𝚕_𝚖𝚒𝚗_𝚟𝚊𝚛$ $(𝙽, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

when $𝙽 \geq | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | - 1$ .

$•$ $𝚙𝚎𝚛𝚖𝚞𝚝𝚊𝚝𝚒𝚘𝚗 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

implies $𝚜𝚞𝚖_𝚌𝚝𝚛$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝙲𝚃𝚁, 𝚅𝙰𝚁)$

when $𝙲𝚃𝚁 \in [=]$

and $𝚅𝙰𝚁 = | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | * (| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | + 1) / 2$ .

$•$ $𝚙𝚎𝚛𝚖𝚞𝚝𝚊𝚝𝚒𝚘𝚗 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

with $| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | > 2$

and $𝚏𝚒𝚛𝚜𝚝 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) >$ $𝚖𝚒𝚗𝚟𝚊𝚕$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛)$

and $𝚕𝚊𝚜𝚝 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) >$ $𝚖𝚒𝚗𝚟𝚊𝚕$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛)$

implies $𝚍𝚎𝚎𝚙𝚎𝚜𝚝_𝚟𝚊𝚕𝚕𝚎𝚢$ $(𝙳𝙴𝙿𝚃𝙷, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

when $𝙳𝙴𝙿𝚃𝙷 =$ $𝚖𝚒𝚗𝚟𝚊𝚕$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛)$ .

$•$ $𝚙𝚎𝚛𝚖𝚞𝚝𝚊𝚝𝚒𝚘𝚗 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

with $| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | > 2$

and $𝚏𝚒𝚛𝚜𝚝 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) = 1$

implies $𝚍𝚎𝚎𝚙𝚎𝚜𝚝_𝚟𝚊𝚕𝚕𝚎𝚢$ $(𝙳𝙴𝙿𝚃𝙷, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

when $𝙳𝙴𝙿𝚃𝙷 = 2$ .

$•$ $𝚙𝚎𝚛𝚖𝚞𝚝𝚊𝚝𝚒𝚘𝚗 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

with $| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | > 2$

and $𝚕𝚊𝚜𝚝 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) = 1$

implies $𝚍𝚎𝚎𝚙𝚎𝚜𝚝_𝚟𝚊𝚕𝚕𝚎𝚢$ $(𝙳𝙴𝙿𝚃𝙷, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

when $𝙳𝙴𝙿𝚃𝙷 = 2$ .

$•$ $𝚙𝚎𝚛𝚖𝚞𝚝𝚊𝚝𝚒𝚘𝚗 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

with $| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | > 2$

and $𝚏𝚒𝚛𝚜𝚝 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) <$ $𝚖𝚊𝚡𝚟𝚊𝚕$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛)$

and $𝚕𝚊𝚜𝚝 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) <$ $𝚖𝚊𝚡𝚟𝚊𝚕$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛)$

implies $𝚑𝚒𝚐𝚑𝚎𝚜𝚝_𝚙𝚎𝚊𝚔$ $(𝙷𝙴𝙸𝙶𝙷𝚃, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

when $𝙷𝙴𝙸𝙶𝙷𝚃 =$ $𝚖𝚊𝚡𝚟𝚊𝚕$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛)$ .

$•$ $𝚙𝚎𝚛𝚖𝚞𝚝𝚊𝚝𝚒𝚘𝚗 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

with $| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | > 2$

and $𝚏𝚒𝚛𝚜𝚝 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) = | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |$

implies $𝚑𝚒𝚐𝚑𝚎𝚜𝚝_𝚙𝚎𝚊𝚔$ $(𝙷𝙴𝙸𝙶𝙷𝚃, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

when $𝙷𝙴𝙸𝙶𝙷𝚃 = | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | - 1$ .

$•$ $𝚙𝚎𝚛𝚖𝚞𝚝𝚊𝚝𝚒𝚘𝚗 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

with $| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | > 2$

and $𝚕𝚊𝚜𝚝 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) = | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |$

implies $𝚑𝚒𝚐𝚑𝚎𝚜𝚝_𝚙𝚎𝚊𝚔$ $(𝙷𝙴𝙸𝙶𝙷𝚃, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

when $𝙷𝙴𝙸𝙶𝙷𝚃 = | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | - 1$ .

Arc input(s)

$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$

Arc generator

𝐶𝐿𝐼𝑄𝑈𝐸

\mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1, 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2)

Arc arity

Arc constraint(s)

𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1 . 𝚟𝚊𝚛 = 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2 . 𝚟𝚊𝚛

Graph property(ies)

𝐌𝐀𝐗_𝐍𝐒𝐂𝐂

\leq 1

Graph class

𝙾𝙽𝙴_𝚂𝚄𝙲𝙲

Graph model

We generate a clique with an equality constraint between each pair of vertices (including a vertex and itself) and state that the size of the largest strongly connected component should not exceed one. Finally the restrictions express the fact that all values are between 1 and the total number of variables.

Parts (A) and (B) of Figure 5.322.1 respectively show the initial and final graph associated with the Example slot. Since we use the $𝐌𝐀𝐗_𝐍𝐒𝐂𝐂$ graph property we show one of the largest strongly connected component of the final graph. The $𝚙𝚎𝚛𝚖𝚞𝚝𝚊𝚝𝚒𝚘𝚗$ holds since all the strongly connected components have at most one vertex: a value is used at most once.

Figure 5.322.1. Initial and final graph of the $𝚙𝚎𝚛𝚖𝚞𝚝𝚊𝚝𝚒𝚘𝚗$ constraint


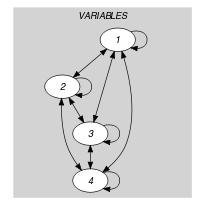
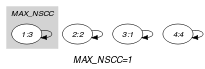
(a)	(b)

Global Constraint Catalog

5. Global Constraint Catalogue

5.322. permutation

Figure 5.322.1. Initial and final graph of the 𝚙𝚎𝚛𝚖𝚞𝚝𝚊𝚝𝚒𝚘𝚗 constraint

Figure 5.322.1. Initial and final graph of the $𝚙𝚎𝚛𝚖𝚞𝚝𝚊𝚝𝚒𝚘𝚗$ constraint