5.156. first_value_diff_0
| DESCRIPTION | LINKS | AUTOMATON |
- Origin
Paparazzi puzzle
- Constraint
- Synonyms
, .
- Arguments
- Restrictions
- Purpose
is equal to the first non-zero variable of the collection .
- Example
-
- Typical
- Arg. properties
Functional dependency: determined by .
- Counting
-
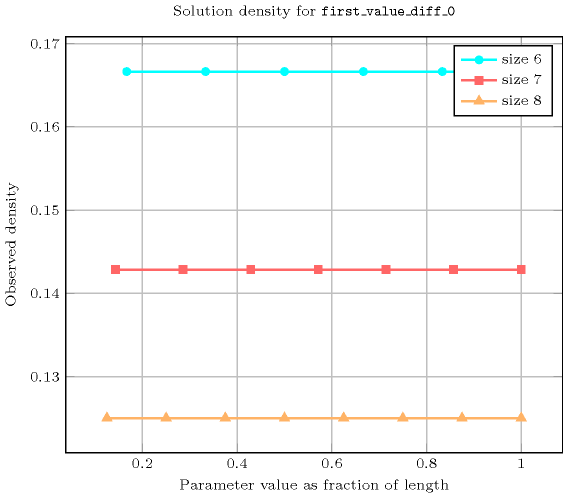
Length () 2 3 4 5 6 7 8 Solutions 8 63 624 7775 117648 2097151 43046720 Number of solutions for : domains
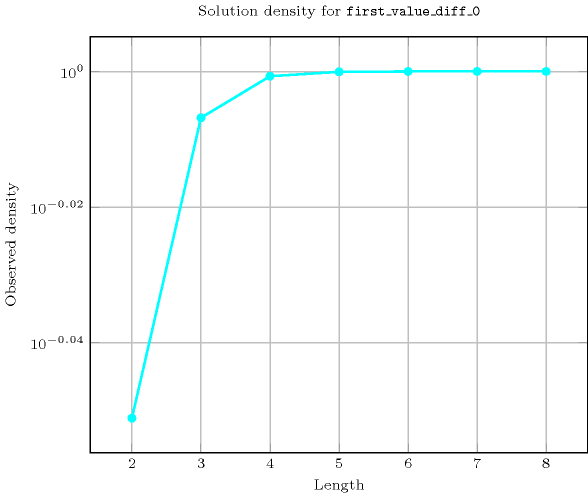
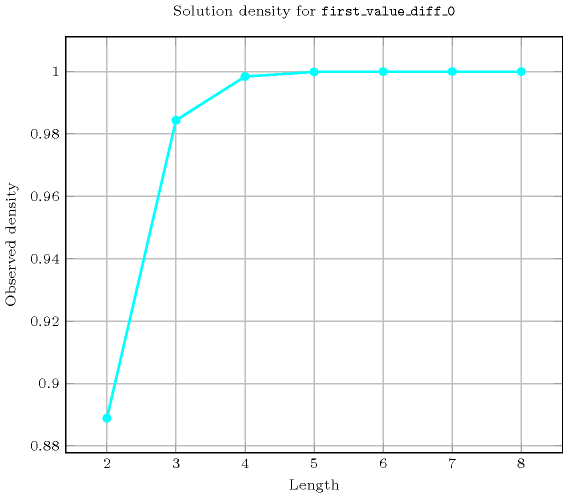
Length () 2 3 4 5 6 7 8 Total 8 63 624 7775 117648 2097151 43046720 Parameter value 1 4 21 156 1555 19608 299593 5380840 2 4 21 156 1555 19608 299593 5380840 3 - 21 156 1555 19608 299593 5380840 4 - - 156 1555 19608 299593 5380840 5 - - - 1555 19608 299593 5380840 6 - - - - 19608 299593 5380840 7 - - - - - 299593 5380840 8 - - - - - - 5380840 Solution count for : domains
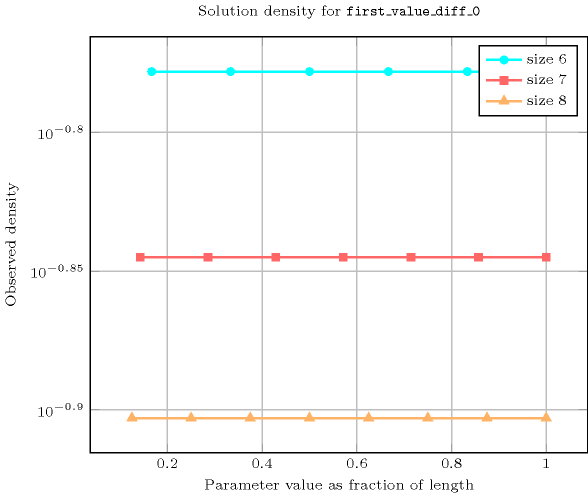
- See also
implies: .
- Keywords
characteristic of a constraint: joker value, automaton, automaton with counters.
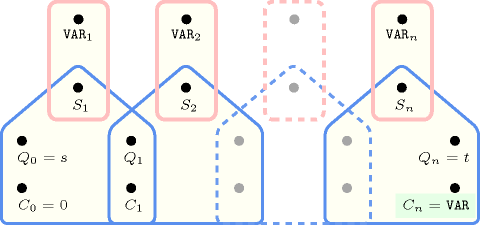
- Automaton
Figure 5.156.1 depicts an automaton that only accepts all the solutions to the constraint. This automaton uses a counter in order to record the value of the first non-zero variable already encountered. To each variable of the collection corresponds a 0-1 signature variable . The following signature constraint links and : .
Figure 5.156.1. Automaton (with one counter) of the constraint
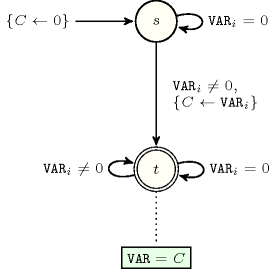
Figure 5.156.2. Hypergraph of the reformulation corresponding to the automaton (with one counter) of the constraint