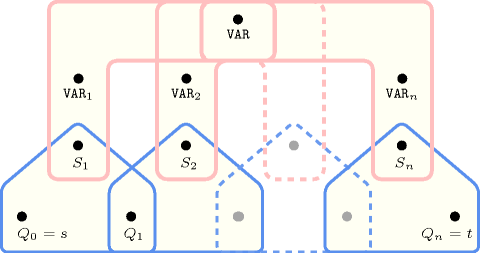
5.50. between_min_max
| DESCRIPTION | LINKS | GRAPH | AUTOMATON |
- Origin
- Constraint
- Arguments
- Restrictions
- Purpose
is greater than or equal to at least one variable of the collection and less than or equal to at least one variable of the collection .
- Example
-
The first constraint holds since its first argument 3 is greater than or equal to the minimum value of the values of the collection and less than or equal to the maximum value of .
- Typical
- Symmetries
Items of are permutable.
can be set to any value of .
- Arg. properties
Extensible wrt. .
- Reformulation
By introducing two extra variables and , the constraint can be expressed in term of the following conjunction of constraints:
,
.
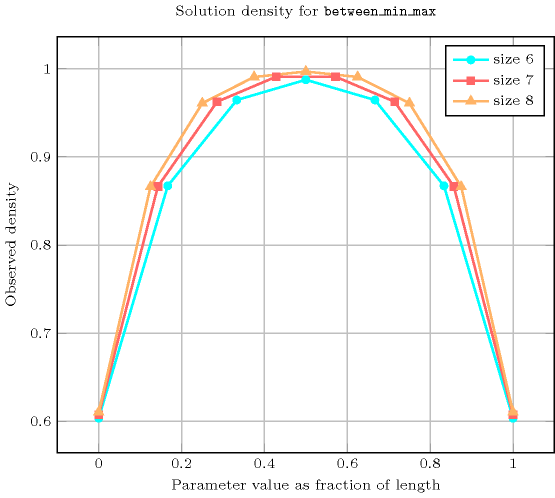
- Counting
-
Length () 2 3 4 5 6 7 8 Solutions 17 184 2417 37806 689201 14376608 338051265 Number of solutions for : domains
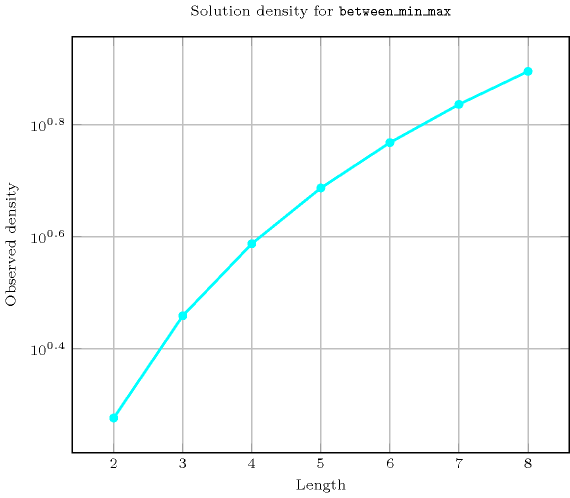
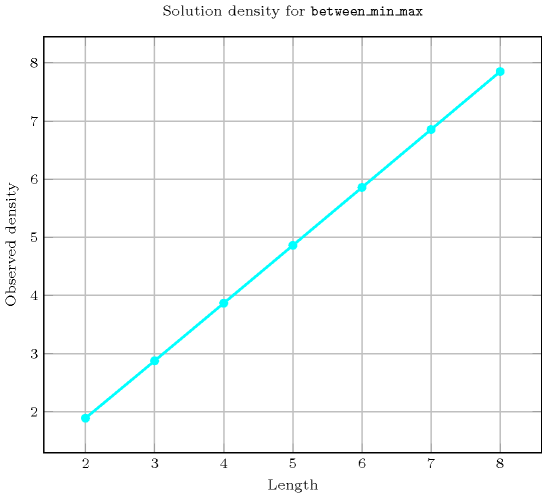
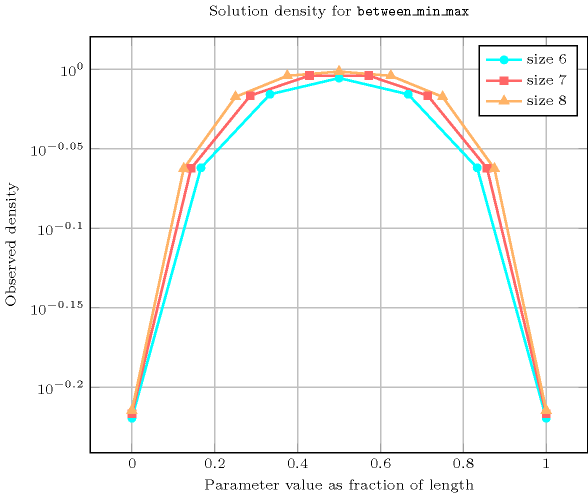
Length () 2 3 4 5 6 7 8 Total 17 184 2417 37806 689201 14376608 338051265 Parameter value 0 5 37 369 4651 70993 1273609 26269505 1 7 55 543 6751 102023 1817215 37281919 2 5 55 593 7501 113489 2018899 41366849 3 - 37 543 7501 116191 2078581 42649535 4 - - 369 6751 113489 2078581 42915649 5 - - - 4651 102023 2018899 42649535 6 - - - - 70993 1817215 41366849 7 - - - - - 1273609 37281919 8 - - - - - - 26269505 Solution count for : domains
- Used in
- See also
implied by: , , , , , , .
- Keywords
characteristic of a constraint: automaton, automaton without counters, reified automaton constraint.
constraint network structure: centered cyclic(1) constraint network(1).
- Derived Collection
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
- Graph property(ies)
-
- Graph class
-
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
- Graph property(ies)
-
- Graph class
-
- Graph model
Parts (A) and (B) of Figure 5.50.1 respectively show the initial and final graph associated with the second graph constraint of the first example of the Example slot. Since we use the graph property, the two arcs of the final graph are stressed in bold. The constraint holds since 3 is greater than 1 and since 3 is less than 8.
Figure 5.50.1. Initial and final graph of the constraint
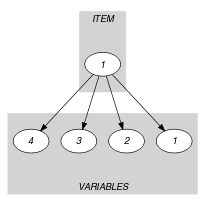
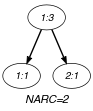
(a) (b)
- Automaton
Figure 5.50.2 depicts the automaton associated with the constraint. To each pair , where is a variable of the collection corresponds a signature variable . The following signature constraint links , and : .
Figure 5.50.2. Automaton of the constraint
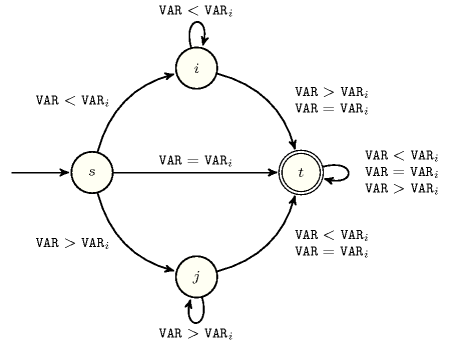
Figure 5.50.3. Hypergraph of the reformulation corresponding to the automaton of the constraint