5.67. circuit_cluster
| DESCRIPTION | LINKS | GRAPH |
- Origin
Inspired by [LaporteAsefVaziriSriskandarajah96].
- Constraint
- Arguments
- Restrictions
- Purpose
Consider a digraph , described by the collection, such that its vertices are partitioned among several clusters. is the number of circuits containing more than one vertex used for covering in such a way that each cluster is visited by exactly one circuit of length greater than 1.
- Example
-
Figure 5.67.1. Four clusters and a covering with one circuit corresponding to the first example of the Example slot
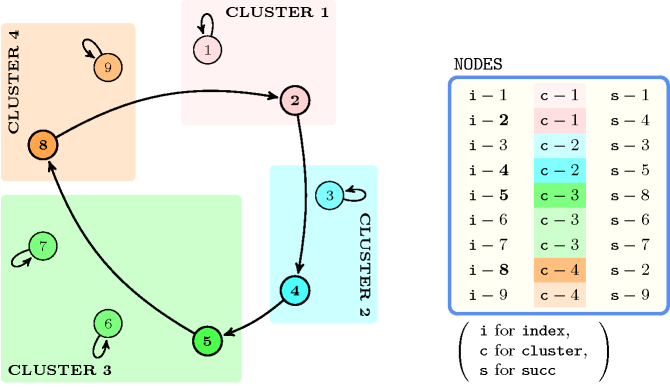
Both examples involve 9 vertices such that vertices 1 and 2 belong to cluster number 1, vertices 3 and 4 belong to cluster number 2, vertices 5, 6 and 7 belong to cluster number 3, and vertices 8 and 9 belong to cluster number 4.
The first example involves only a single circuit containing more than one vertex (i.e., see in Figure 5.67.1 the circuit ). The corresponding constraint holds since exactly one vertex of each cluster (i.e., vertex 2 for cluster 1, vertex 4 for cluster 2, vertex 5 for cluster 3, vertex 8 for cluster 4) belongs to this circuit.
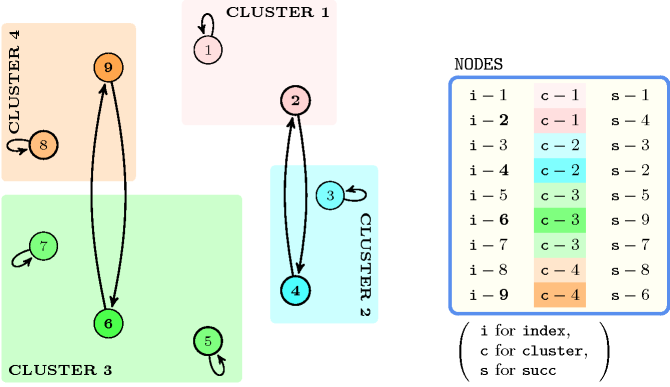
The second example contains the two circuits and that both involve more than one vertex. The corresponding constraint holds since exactly one vertex of each cluster (i.e., see in Figure 5.67.2 vertex 2 in for cluster 1, vertex 4 in for cluster 2, vertex 6 in for cluster 3, vertex 9 in for cluster 4) belongs to these two circuits.
Figure 5.67.2. The same clusters as in the first example of the Example slot and a covering with two circuits corresponding to the second example of the Example slot
- Typical
- Symmetry
Items of are permutable.
- Usage
A related abstraction in Operations Research was introduced in [LaporteAsefVaziriSriskandarajah96]. It was reported as the Generalised Travelling Salesman Problem (GTSP). The constraint differs from the GTSP because of the two following points:
Each node of our graph belongs to a single cluster,
We do not constrain the number of circuits to be equal to 1: The number of circuits should be equal to one of the values of the domain of the variable .
- See also
common keyword: (permutation), , (graph constraint, one_succ).
- Keywords
combinatorial object: permutation.
constraint type: graph constraint.
final graph structure: strongly connected component, one_succ.
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
-
- Graph property(ies)
-
- Graph class
-
- Sets
-
- Constraint(s) on sets
-
- Graph model
In order to express the binary constraint linking two vertices one has to make explicit the identifier of each vertex as well as the cluster to which belongs each vertex. This is why the constraint considers objects that have the following three attributes:
The attribute that is the identifier of a vertex.
The attribute that is the cluster to which belongs a vertex.
The attribute that is the unique successor of a vertex.
The partitioning of the clusters by different circuits is expressed in the following way:
First note the condition prevents the final graph of containing any loop. Moreover the condition imposes no more than one successor for each vertex of the final graph.
The graph property 0 enforces that all vertices of the final graph belong to one circuit.
The graph property express the fact that the number of strongly connected components of the final graph is equal to .
The constraint on the set (i.e., all the vertices of the final graph) states that the cluster attributes of the vertices of the final graph should be pairwise distinct. This concretely means that no cluster should be visited more than once.
The constraint on the set conveys the fact that the number of distinct values of the cluster attribute of the vertices of the final graph should be equal to the total number of clusters. This implies that each cluster is visited at least one time.
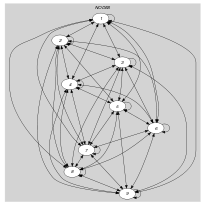
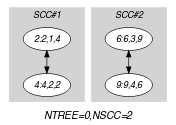
Parts (A) and (B) of Figure 5.67.3 respectively show the initial and final graph associated with the second example of the Example slot. Since we use the graph property, we show the two strongly connected components of the final graph. They respectively correspond to the two circuits and . Since all the vertices belongs to a circuit we have that 0.
Figure 5.67.3. Initial and final graph of the constraint
(a) (b)