5.207. k_same
| DESCRIPTION | LINKS | GRAPH |
- Origin
- Constraint
- Type
- Argument
- Restrictions
- Purpose
Given sets, each containing the same number of domain variables, the constraint forces that the multisets of values assigned to each set are all identical.
- Example
-
The constraint holds since:
The first and second collections of variables are assigned to the same multiset.
The second and third collections of variables are also assigned to the same multiset.
- Typical
- Symmetries
Items of are permutable.
Items of are permutable.
All occurrences of two distinct values of can be swapped; all occurrences of a value of can be renamed to any unused value.
- Arg. properties
Contractible wrt. .
- Remark
It was shown in [ElbassioniKatrielKutzMahajan05] that, finding out whether the constraint has a solution or not is NP-hard when we have more than one constraint. This was achieved by reduction from 3-dimensional-matching in the context where we have 2 constraints.
- See also
common keyword: , , (system of constraints).
implies: .
- Keywords
characteristic of a constraint: sort based reformulation.
combinatorial object: permutation, multiset.
complexity: 3-dimensional-matching.
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
- Graph property(ies)
-
- Graph model
Parts (A) and (B) of Figure 5.207.1 respectively show the initial and final graph associated with the Example slot. To each vertex corresponds a collection of variables, while to each arc corresponds a constraint.
Figure 5.207.1. Initial and final graph of the constraint
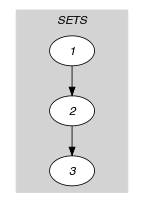
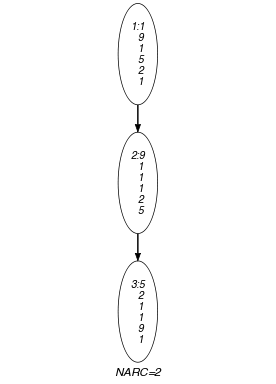
(a) (b)