5.374. stage_element
| DESCRIPTION | LINKS | GRAPH | AUTOMATON |
- Origin
- Constraint
- Usual name
- Synonym
.
- Arguments
- Restrictions
- Purpose
Let , and respectively denote the values of the , and attributes of the item of the collection. First we have that: and .
Second, the constraint forces the following equivalence:
.
- Example
-
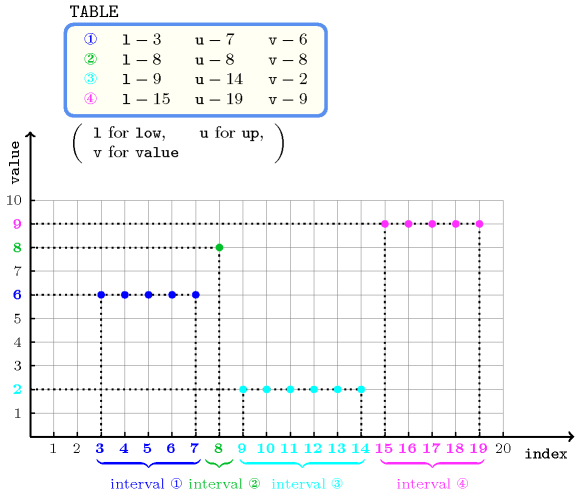
FigureΒ 5.374.1 depicts the function associated with the items of the collection. The constraint holds since:
The value of is located between the values of the and attributes of the first item of the collection (i.e.,Β ).
The value of corresponds to the attribute of the first item of the collection (i.e.,Β 6).
Figure 5.374.1. Function defined on four intervals β , β‘, β’ and β£ associated with the collection of the Example slot for linking the and attributes of the collection
- Typical
- Symmetry
All occurrences of two distinct values in or can be swapped; all occurrences of a value in or can be renamed to any unused value.
- Arg. properties
Functional dependency: determined by and .
Suffix-extensible wrt. .
- See also
common keyword: , Β (data constraint).
- Keywords
characteristic of a constraint: automaton, automaton without counters, reified automaton constraint.
constraint arguments: binary constraint, pure functional dependency.
constraint network structure: centered cyclic(2) constraint network(1).
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
-
- Graph property(ies)
-
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
-
- Graph property(ies)
-
- Graph model
The first graph constraint models the restrictions on the and attributes of the collection, while the second graph constraint is similar to the one used for defining the constraint.
PartsΒ (A) andΒ (B) of FigureΒ 5.374.2 respectively show the initial and final graph associated with the second graph constraint of the Example slot. Since we use the graph property, the unique arc of the final graph is stressed in bold.
Figure 5.374.2. Initial and final graph of the constraint
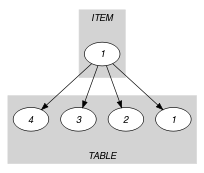
(a) (b)
- Automaton
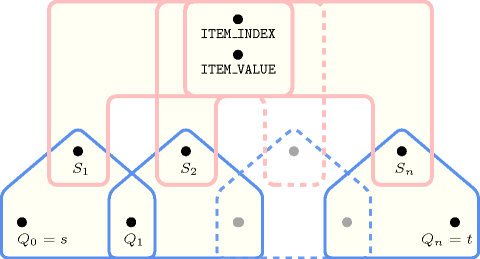
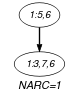
FigureΒ 5.374.3 depicts the automaton associated with the constraint. Let and respectively be the and the attributes of the unique item of the collection. Let , and respectively be the , the and the attributes of the item of the collection. To each quintuple corresponds a 0-1 signature variable as well as the following signature constraint: .
Figure 5.374.3. Automaton of the constraint
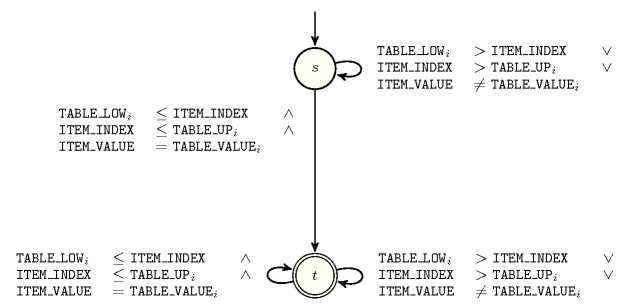
Figure 5.374.4. Hypergraph of the reformulation corresponding to the automaton of the constraint
