5.293. nvisible_from_start
| DESCRIPTION | LINKS | AUTOMATON |
- Origin
Derived from a puzzle called skyscraper
- Constraint
- Synonyms
, .
- Arguments
- Restrictions
- Purpose
The variable of the sequence is visible if and only if all variables before the variable are strictly smaller than the variable itself. is the total number of visible variables of the sequence of variables .
- Example
-
The first constraint holds since the sequence contains three visible items that respectively correspond to the first, second and sixth items.
- Typical
- Symmetry
One and the same constant can be added to the attribute of all items of .
- Arg. properties
Functional dependency: determined by .
- Counting
-
Length () 2 3 4 5 6 7 8 Solutions 9 64 625 7776 117649 2097152 43046721 Number of solutions for : domains
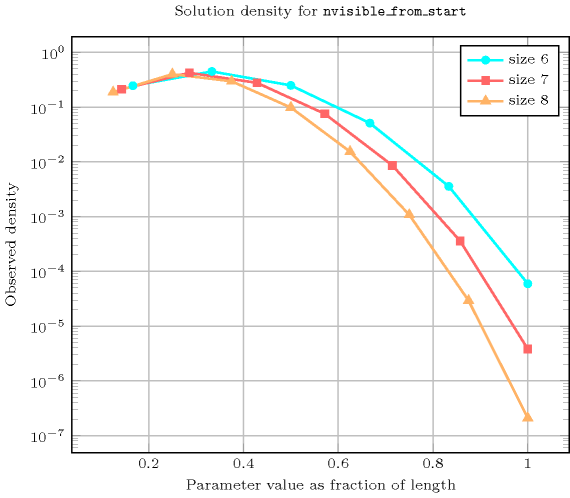
Length () 2 3 4 5 6 7 8 Total 9 64 625 7776 117649 2097152 43046721 Parameter value 1 6 30 225 2275 29008 446964 8080425 2 3 30 305 3675 52794 889056 17238570 3 - 4 90 1610 29400 583548 12780180 4 - - 5 210 6020 158760 4238367 5 - - - 6 420 18060 661500 6 - - - - 7 756 46410 7 - - - - - 8 1260 8 - - - - - - 9 Solution count for : domains
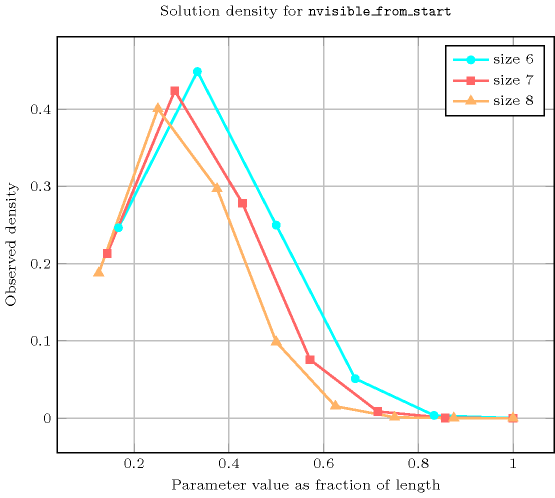
- See also
-
implies: .
related: (count from the end of the sequence rather than from the start).
- Keywords
combinatorial object: sequence.
- Automaton
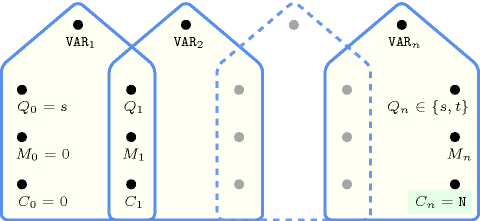
Figure 5.293.1 depicts the automaton associated with the constraint.
Figure 5.293.1. Automaton of the constraint with two counters and , where records the largest value encountered so far, and the number of visible values from the left hand side of the sequence , , ...,
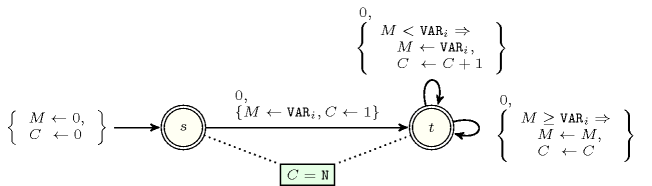
Figure 5.293.2. Hypergraph of the reformulation corresponding to the automaton (with two counters) of the constraint (since all states of the automaton are accepting there is no restriction on the last variable )