5.102. cutset
| DESCRIPTION | LINKS | GRAPH |
- Origin
- Constraint
- Arguments
- Restrictions
- Purpose
Consider a digraph with vertices described by the collection. Enforces that the subset of kept vertices of cardinality and their corresponding arcs form a graph without circuit.
- Example
-
The constraint holds since the vertices of the collection for which the attribute is set to 1 correspond to a graph without circuit and since exactly one () vertex has its attribute set to 0.
- Typical
- Symmetry
Items of are permutable.
- Usage
The article [FagesLal03] introducing the constraint mentions applications from various areas such that deadlock breaking or program verification.
- Remark
The undirected version of the constraint corresponds to the minimum feedback vertex set problem.
- Algorithm
The filtering algorithm presented in [FagesLal03] uses graph reduction techniques inspired from Levy and Low [LevyLow88] as well as from Lloyd, Soffa and Wang [LloydSoffaWang88].
- Keywords
application area: deadlock breaking, program verification.
constraint type: graph constraint.
final graph structure: circuit, directed acyclic graph, acyclic, no loop.
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
-
- Graph property(ies)
-
- Graph class
-
- Graph model
We use a set of integers for representing the successors of each vertex. Because of the arc constraint, all arcs such that the attribute of one extremity is equal to 0 are eliminated; Therefore all vertices for which the attribute is equal to 0 are also eliminated (since they will correspond to isolated vertices). The graph property 1 enforces the size of the largest strongly connected component to not exceed 1; Therefore, the final graph cannot contain any circuit.
Part (A) of Figure 5.102.1 shows the initial graph from which we have chosen to start. It is derived from the set associated with each vertex. Each set describes the potential values of the attribute of a given vertex. Part (B) of Figure 5.102.1 gives the final graph associated with the Example slot. Since we use the graph property, the vertices of the final graph are stressed in bold. The constraint holds since the final graph does not contain any circuit and since the number of removed vertices is equal to 1.
Figure 5.102.1. Initial and final graph of the set constraint
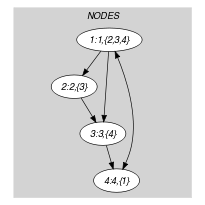
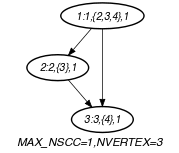
(a) (b)