Global Constraint Catalog: Ccorrespondence

5.90. correspondence

DESCRIPTION

LINKS

GRAPH

Origin

Derived from $𝚜𝚘𝚛𝚝_𝚙𝚎𝚛𝚖𝚞𝚝𝚊𝚝𝚒𝚘𝚗$ by removing the sorting condition.

Constraint

$𝚌𝚘𝚛𝚛𝚎𝚜𝚙𝚘𝚗𝚍𝚎𝚗𝚌𝚎 (𝙵𝚁𝙾𝙼, 𝙿𝙴𝚁𝙼𝚄𝚃𝙰𝚃𝙸𝙾𝙽, 𝚃𝙾)$

Arguments

$𝙵𝚁𝙾𝙼$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚏𝚛𝚘𝚖 - 𝚍𝚟𝚊𝚛)$
$𝙿𝙴𝚁𝙼𝚄𝚃𝙰𝚃𝙸𝙾𝙽$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)$
$𝚃𝙾$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚝𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)$

Restrictions

| 𝙿𝙴𝚁𝙼𝚄𝚃𝙰𝚃𝙸𝙾𝙽 | = | 𝙵𝚁𝙾𝙼 |

| 𝙿𝙴𝚁𝙼𝚄𝚃𝙰𝚃𝙸𝙾𝙽 | = | 𝚃𝙾 |

𝙿𝙴𝚁𝙼𝚄𝚃𝙰𝚃𝙸𝙾𝙽 . 𝚟𝚊𝚛 \geq 1

𝙿𝙴𝚁𝙼𝚄𝚃𝙰𝚃𝙸𝙾𝙽 . 𝚟𝚊𝚛 \leq | 𝙿𝙴𝚁𝙼𝚄𝚃𝙰𝚃𝙸𝙾𝙽 |

𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝

(𝙿𝙴𝚁𝙼𝚄𝚃𝙰𝚃𝙸𝙾𝙽)

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝙵𝚁𝙾𝙼, 𝚏𝚛𝚘𝚖)

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝙿𝙴𝚁𝙼𝚄𝚃𝙰𝚃𝙸𝙾𝙽, 𝚟𝚊𝚛)

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚃𝙾, 𝚝𝚟𝚊𝚛)

Purpose

The variables of collection $𝙵𝚁𝙾𝙼$ correspond to the variables of collection $𝚃𝙾$ according to the permutation $𝙿𝙴𝚁𝙼𝚄𝚃𝙰𝚃𝙸𝙾𝙽$ (i.e., $𝙵𝚁𝙾𝙼 [i] . 𝚏𝚛𝚘𝚖 = 𝚃𝙾 [𝙿𝙴𝚁𝙼𝚄𝚃𝙰𝚃𝙸𝙾𝙽 [i] . 𝚟𝚊𝚛] . 𝚝𝚟𝚊𝚛$ ).

Example

(〈1, 9, 1, 5, 2, 1〉, 〈6, 1, 3, 5, 4, 2〉, 〈9, 1, 1, 2, 5, 1〉)

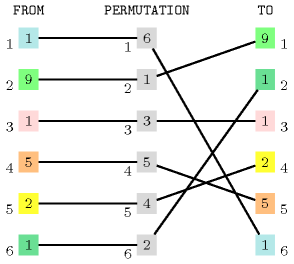
As illustrated by Figure 5.90.1, the $𝚌𝚘𝚛𝚛𝚎𝚜𝚙𝚘𝚗𝚍𝚎𝚗𝚌𝚎$ constraint holds since:

The first item $𝙵𝚁𝙾𝙼 [1] . 𝚏𝚛𝚘𝚖 = 1$ of collection $𝙵𝚁𝙾𝙼$ corresponds to the $𝙿𝙴𝚁𝙼𝚄𝚃𝙰𝚃𝙸𝙾𝙽 [1] . 𝚟𝚊𝚛 = 6^{t h}$ item of collection $𝚃𝙾$ .
The second item $𝙵𝚁𝙾𝙼 [2] . 𝚏𝚛𝚘𝚖 = 9$ of collection $𝙵𝚁𝙾𝙼$ corresponds to the $𝙿𝙴𝚁𝙼𝚄𝚃𝙰𝚃𝙸𝙾𝙽 [2] . 𝚟𝚊𝚛 = 1^{t h}$ item of collection $𝚃𝙾$ .
The third item $𝙵𝚁𝙾𝙼 [3] . 𝚏𝚛𝚘𝚖 = 1$ of collection $𝙵𝚁𝙾𝙼$ corresponds to the $𝙿𝙴𝚁𝙼𝚄𝚃𝙰𝚃𝙸𝙾𝙽 [3] . 𝚟𝚊𝚛 = 3^{t h}$ item of collection $𝚃𝙾$ .
The fourth item $𝙵𝚁𝙾𝙼 [4] . 𝚏𝚛𝚘𝚖 = 5$ of collection $𝙵𝚁𝙾𝙼$ corresponds to the $𝙿𝙴𝚁𝙼𝚄𝚃𝙰𝚃𝙸𝙾𝙽 [4] . 𝚟𝚊𝚛 = 5^{t h}$ item of collection $𝚃𝙾$ .
The fifth item $𝙵𝚁𝙾𝙼 [5] . 𝚏𝚛𝚘𝚖 = 2$ of collection $𝙵𝚁𝙾𝙼$ corresponds to the $𝙿𝙴𝚁𝙼𝚄𝚃𝙰𝚃𝙸𝙾𝙽 [5] . 𝚟𝚊𝚛 = 4^{t h}$ item of collection $𝚃𝙾$ .
The sixth item $𝙵𝚁𝙾𝙼 [6] . 𝚏𝚛𝚘𝚖 = 1$ of collection $𝙵𝚁𝙾𝙼$ corresponds to the $𝙿𝙴𝚁𝙼𝚄𝚃𝙰𝚃𝙸𝙾𝙽 [6] . 𝚟𝚊𝚛 = 2^{t h}$ item of collection $𝚃𝙾$ .

Figure 5.90.1. Illustration of the correspondence between the items of the $𝙵𝚁𝙾𝙼$ and the $𝚃𝙾$ collections according to the permutation defined by the items of the $𝙿𝙴𝚁𝙼𝚄𝚃𝙰𝚃𝙸𝙾𝙽$ collection of the Example slot

Typical

| 𝙵𝚁𝙾𝙼 | > 1

𝚛𝚊𝚗𝚐𝚎

(𝙵𝚁𝙾𝙼 . 𝚏𝚛𝚘𝚖) > 1

Symmetry

All occurrences of two distinct values in $𝙵𝚁𝙾𝙼 . 𝚏𝚛𝚘𝚖$ or $𝚃𝙾 . 𝚝𝚟𝚊𝚛$ can be swapped; all occurrences of a value in $𝙵𝚁𝙾𝙼 . 𝚏𝚛𝚘𝚖$ or $𝚃𝙾 . 𝚝𝚟𝚊𝚛$ can be renamed to any unused value.

Remark

Similar to the $𝚜𝚊𝚖𝚎$ constraint except that we also provide the permutation that allows to go from the items of collection $𝙵𝚁𝙾𝙼$ to the items of collection $𝚃𝙾$ .

Algorithm

An arc-consistency filtering algorithm for the $𝚌𝚘𝚛𝚛𝚎𝚜𝚙𝚘𝚗𝚍𝚎𝚗𝚌𝚎$ constraint is described in [Cymer12], [CymerPhD13]. The algorithm is based on the following ideas:

First, one can map solutions to the $𝚌𝚘𝚛𝚛𝚎𝚜𝚙𝚘𝚗𝚍𝚎𝚗𝚌𝚎$ constraint to perfect matchings in a bipartite graph derived from the domain of the variables of the constraint in the following way: to each variable of the $𝙵𝚁𝙾𝙼$ collection there is a from vertex; similarly, to each variable of the $𝚃𝙾$ collection there is a to vertex; finally, there is an edge between the $i^{t h}$ from vertex and the $j^{t h}$ to vertex if and only if the corresponding domains intersect and if $j$ belongs to the domain of the $i^{t h}$ permutation variable.
Second, Dulmage-Mendelsohn decomposition [DulmageMendelsohn58] is used to characterise all edges that do not belong to any perfect matching, and therefore prune the corresponding variables.

See also

implied by: $𝚜𝚘𝚛𝚝_𝚙𝚎𝚛𝚖𝚞𝚝𝚊𝚝𝚒𝚘𝚗$ .

specialisation: $𝚜𝚊𝚖𝚎$ ( $𝙿𝙴𝚁𝙼𝚄𝚃𝙰𝚃𝙸𝙾𝙽$ parameter removed).

Keywords

characteristic of a constraint: derived collection.

combinatorial object: permutation.

constraint arguments: constraint between three collections of variables.

filtering: bipartite matching.

final graph structure: acyclic, bipartite, no loop.

Derived Collection

𝚌𝚘𝚕 (\begin{matrix} 𝙵𝚁𝙾𝙼_𝙿𝙴𝚁𝙼𝚄𝚃𝙰𝚃𝙸𝙾𝙽 - 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚏𝚛𝚘𝚖 - 𝚍𝚟𝚊𝚛, 𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛), \\ 𝚒𝚝𝚎𝚖 (𝚏𝚛𝚘𝚖 - 𝙵𝚁𝙾𝙼 . 𝚏𝚛𝚘𝚖, 𝚟𝚊𝚛 - 𝙿𝙴𝚁𝙼𝚄𝚃𝙰𝚃𝙸𝙾𝙽 . 𝚟𝚊𝚛)] \end{matrix})

Arc input(s)

$𝙵𝚁𝙾𝙼_𝙿𝙴𝚁𝙼𝚄𝚃𝙰𝚃𝙸𝙾𝙽$ $𝚃𝙾$

Arc generator

𝑃𝑅𝑂𝐷𝑈𝐶𝑇

\mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚏𝚛𝚘𝚖_𝚙𝚎𝚛𝚖𝚞𝚝𝚊𝚝𝚒𝚘𝚗, 𝚝𝚘)

Arc arity

Arc constraint(s)

• 𝚏𝚛𝚘𝚖_𝚙𝚎𝚛𝚖𝚞𝚝𝚊𝚝𝚒𝚘𝚗 . 𝚏𝚛𝚘𝚖 = 𝚝𝚘 . 𝚝𝚟𝚊𝚛

• 𝚏𝚛𝚘𝚖_𝚙𝚎𝚛𝚖𝚞𝚝𝚊𝚝𝚒𝚘𝚗 . 𝚟𝚊𝚛 = 𝚝𝚘 . 𝚔𝚎𝚢

Graph property(ies)

𝐍𝐀𝐑𝐂

= | 𝙿𝙴𝚁𝙼𝚄𝚃𝙰𝚃𝙸𝙾𝙽 |

Graph class

•

𝙰𝙲𝚈𝙲𝙻𝙸𝙲

•

𝙱𝙸𝙿𝙰𝚁𝚃𝙸𝚃𝙴

•

𝙽𝙾_𝙻𝙾𝙾𝙿

Graph model

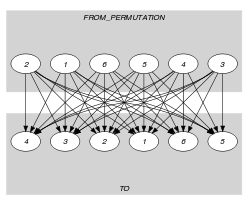
Parts (A) and (B) of Figure 5.90.2 respectively show the initial and final graph associated with the Example slot. In both graphs the source vertices correspond to the derived collection $𝙵𝚁𝙾𝙼_𝙿𝙴𝚁𝙼𝚄𝚃𝙰𝚃𝙸𝙾𝙽$ , while the sink vertices correspond to the collection $𝚃𝙾$ . Since the final graph contains exactly $| 𝙿𝙴𝚁𝙼𝚄𝚃𝙰𝚃𝙸𝙾𝙽 |$ arcs the $𝚌𝚘𝚛𝚛𝚎𝚜𝚙𝚘𝚗𝚍𝚎𝚗𝚌𝚎$ constraint holds. As we use the $𝐍𝐀𝐑𝐂$ graph property, the arcs of the final graph are stressed in bold.

Figure 5.90.2. Initial and final graph of the $𝚌𝚘𝚛𝚛𝚎𝚜𝚙𝚘𝚗𝚍𝚎𝚗𝚌𝚎$ constraint

(a)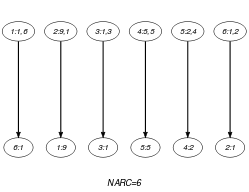

(b)

Signature

Because of the second condition $𝚏𝚛𝚘𝚖_𝚙𝚎𝚛𝚖𝚞𝚝𝚊𝚝𝚒𝚘𝚗 . 𝚟𝚊𝚛 = 𝚝𝚘 . 𝚔𝚎𝚢$ of the arc constraint and since both, the $𝚟𝚊𝚛$ attributes of the collection $𝙵𝚁𝙾𝙼_𝙿𝙴𝚁𝙼𝚄𝚃𝙰𝚃𝙸𝙾𝙽$ and the $𝚔𝚎𝚢$ attributes of the collection $𝚃𝙾$ are all-distinct, the final graph contains at most $| 𝙿𝙴𝚁𝙼𝚄𝚃𝙰𝚃𝙸𝙾𝙽 |$ arcs. Therefore we can rewrite the graph property $𝐍𝐀𝐑𝐂$ $=$ $| 𝙿𝙴𝚁𝙼𝚄𝚃𝙰𝚃𝙸𝙾𝙽 |$ to $𝐍𝐀𝐑𝐂$ $\geq$ $| 𝙿𝙴𝚁𝙼𝚄𝚃𝙰𝚃𝙸𝙾𝙽 |$ . This leads to simplify $\underset{̲}{\bar{𝐍𝐀𝐑𝐂}}$ to $\bar{𝐍𝐀𝐑𝐂}$ .

Global Constraint Catalog

5. Global Constraint Catalogue

5.90. correspondence

Figure 5.90.1. Illustration of the correspondence between the items of the 𝙵𝚁𝙾𝙼 and the 𝚃𝙾 collections according to the permutation defined by the items of the 𝙿𝙴𝚁𝙼𝚄𝚃𝙰𝚃𝙸𝙾𝙽 collection of the Example slot

Figure 5.90.2. Initial and final graph of the 𝚌𝚘𝚛𝚛𝚎𝚜𝚙𝚘𝚗𝚍𝚎𝚗𝚌𝚎 constraint

Figure 5.90.1. Illustration of the correspondence between the items of the $𝙵𝚁𝙾𝙼$ and the $𝚃𝙾$ collections according to the permutation defined by the items of the $𝙿𝙴𝚁𝙼𝚄𝚃𝙰𝚃𝙸𝙾𝙽$ collection of the Example slot

Figure 5.90.2. Initial and final graph of the $𝚌𝚘𝚛𝚛𝚎𝚜𝚙𝚘𝚗𝚍𝚎𝚗𝚌𝚎$ constraint