5.292. nvisible_from_end
| DESCRIPTION | LINKS | AUTOMATON |
- Origin
- Constraint
- Synonyms
, .
- Arguments
- Restrictions
- Purpose
The variable of the sequence is visible if and only if all variables after the variable are strictly smaller than the variable itself. is the total number of visible variables of the sequence of variables .
- Example
-
The first constraint holds since the sequence contains two visible items that respectively correspond to the seventh and sixth items.
- Typical
- Symmetry
One and the same constant can be added to the attribute of all items of .
- Arg. properties
Functional dependency: determined by .
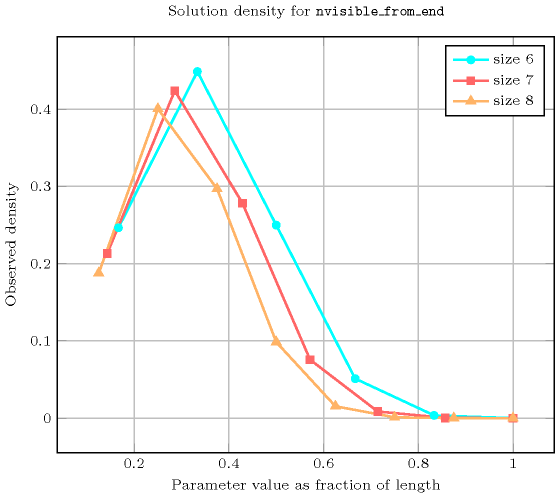
- Counting
-
Length () 2 3 4 5 6 7 8 Solutions 9 64 625 7776 117649 2097152 43046721 Number of solutions for : domains
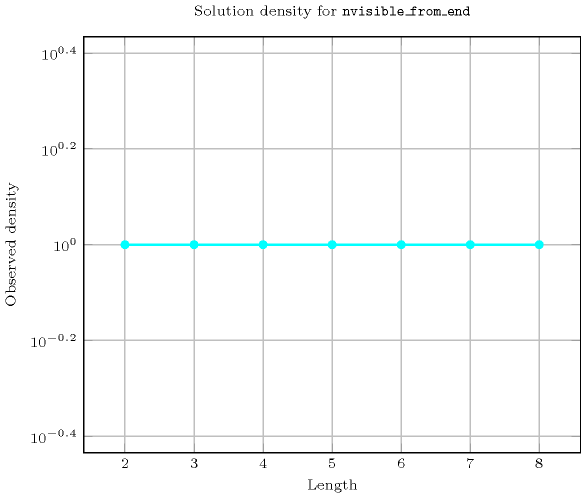
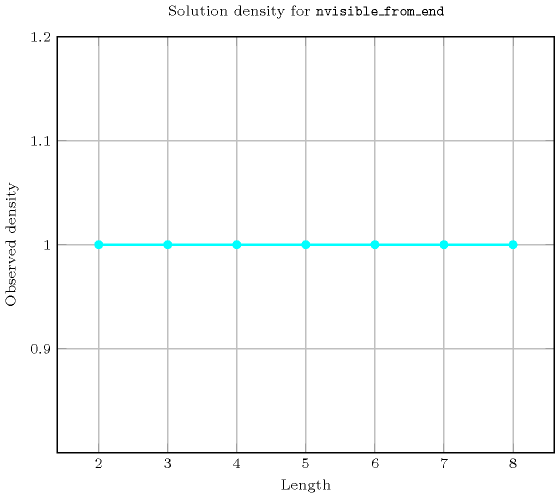
Length () 2 3 4 5 6 7 8 Total 9 64 625 7776 117649 2097152 43046721 Parameter value 1 6 30 225 2275 29008 446964 8080425 2 3 30 305 3675 52794 889056 17238570 3 - 4 90 1610 29400 583548 12780180 4 - - 5 210 6020 158760 4238367 5 - - - 6 420 18060 661500 6 - - - - 7 756 46410 7 - - - - - 8 1260 8 - - - - - - 9 Solution count for : domains
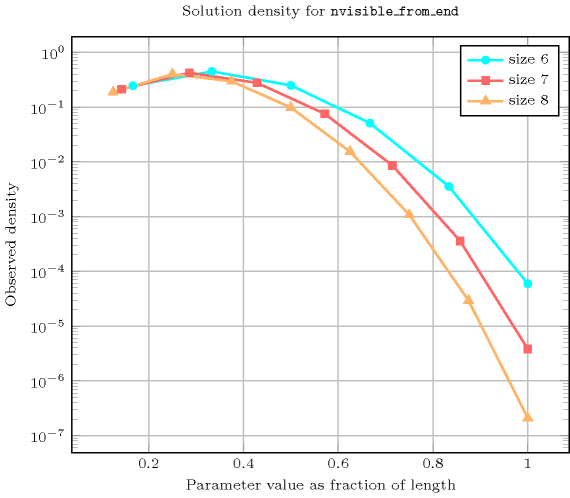
- See also
implies: .
related: (count from the start of the sequence rather than from the end).
- Keywords
combinatorial object: sequence.
- Automaton
Figure 5.292.1 depicts the automaton associated with the constraint.
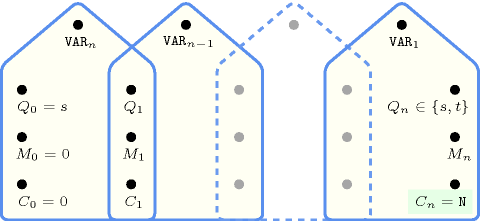
Figure 5.292.1. Automaton of the constraint with two counters and , where records the largest value encountered so far, and the number of visible values from the right hand side of the sequence , , ..., (i.e., the sequence , , ..., is passed to the automaton)
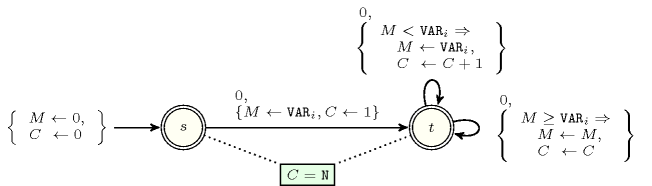
Figure 5.292.2. Hypergraph of the reformulation corresponding to the automaton (with two counters) of the constraint (since all states of the automaton are accepting there is no restriction on the last variable )