5.24. among_diff_0
| DESCRIPTION | LINKS | GRAPH | AUTOMATON |
- Origin
- Constraint
- Arguments
- Restrictions
- Purpose
is the number of variables of the collection that take a value different from 0.
- Example
-
The first constraint holds since exactly 3 values of the collection of values are different from 0.
- Typical
- Symmetries
Items of are permutable.
An occurrence of a value of that is different from 0 can be replaced by any other value that is also different from 0.
- Arg. properties
Functional dependency: determined by .
Contractible wrt. when .
Contractible wrt. when .
Aggregate: , .
- Counting
-
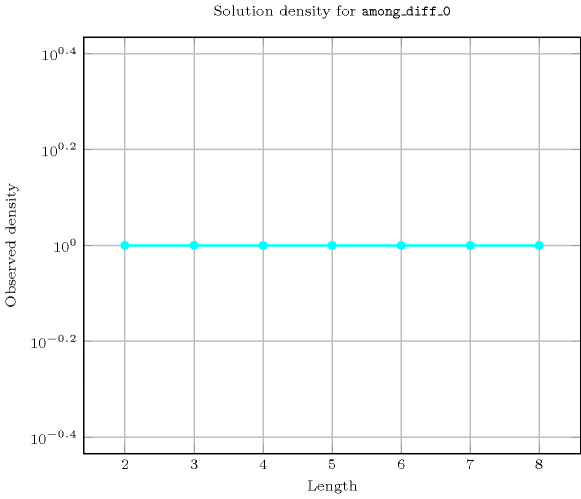
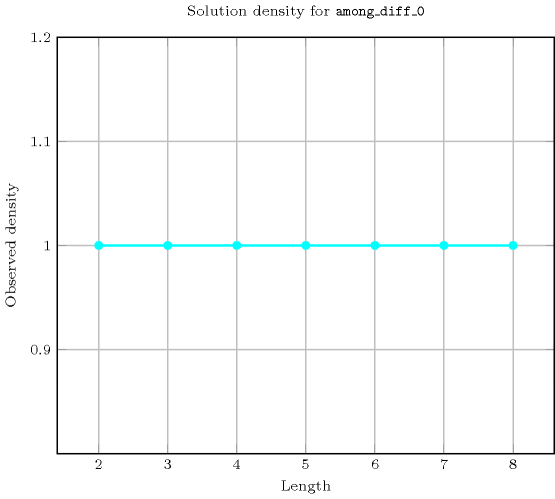
Length () 2 3 4 5 6 7 8 Solutions 9 64 625 7776 117649 2097152 43046721 Number of solutions for : domains
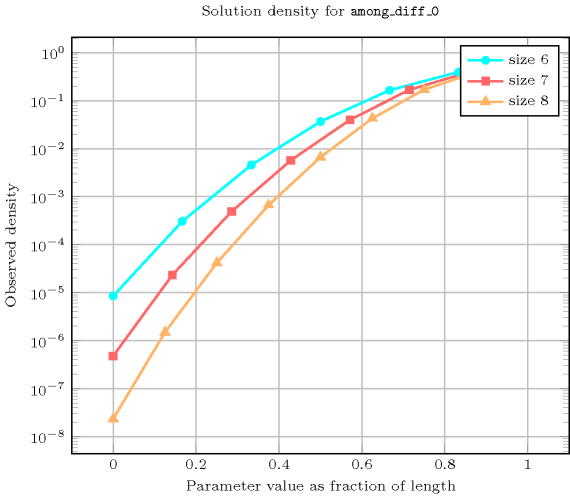
Length () 2 3 4 5 6 7 8 Total 9 64 625 7776 117649 2097152 43046721 Parameter value 0 1 1 1 1 1 1 1 1 4 9 16 25 36 49 64 2 4 27 96 250 540 1029 1792 3 - 27 256 1250 4320 12005 28672 4 - - 256 3125 19440 84035 286720 5 - - - 3125 46656 352947 1835008 6 - - - - 46656 823543 7340032 7 - - - - - 823543 16777216 8 - - - - - - 16777216 Solution count for : domains
- See also
common keyword: (counting constraint).
generalisation: ( replaced by ).
- Keywords
characteristic of a constraint: joker value, automaton, automaton with counters.
constraint arguments: pure functional dependency.
constraint network structure: alpha-acyclic constraint network(2).
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
- Graph property(ies)
-
- Graph model
Since this is a unary constraint we employ the arc generator in order to produce an initial graph with a single loop on each vertex.
Parts (A) and (B) of Figure 5.24.1 respectively show the initial and final graph associated with first example of the Example slot. Since we use the graph property, the loops of the final graph are stressed in bold.
Figure 5.24.1. Initial and final graph of the constraint

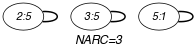
(a) (b)
- Automaton
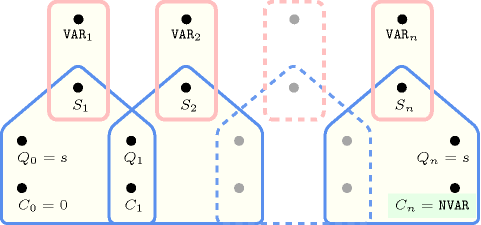
Figure 5.24.2 depicts the automaton associated with the constraint. To each variable of the collection corresponds a 0-1 signature variable . The following signature constraint links and : . The automaton counts the number of variables of the collection that take a value different from 0 and finally assigns this number to .
Figure 5.24.2. Automaton of the constraint
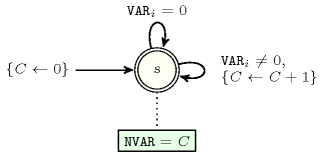
Figure 5.24.3. Hypergraph of the reformulation corresponding to the automaton (with one counter) of the constraint: since all states variables are fixed to the unique state of the automaton, the transitions constraints share only the counter variable and the constraint network is Berge-acyclic