Global Constraint Catalog: Cith_pos_different_from

5.203. ith_pos_different_from_0

DESCRIPTION

LINKS

AUTOMATON

Origin

N. Beldiceanu

Constraint

$𝚒𝚝𝚑_𝚙𝚘𝚜_𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚏𝚛𝚘𝚖_0 (𝙸𝚃𝙷, 𝙿𝙾𝚂, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

Arguments

Restrictions

𝙸𝚃𝙷 \geq 1

𝙸𝚃𝙷 \leq | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |

𝙿𝙾𝚂 \geq 𝙸𝚃𝙷

𝙿𝙾𝚂 \leq | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚟𝚊𝚛)

Purpose

$𝙿𝙾𝚂$ is the position of the ${𝙸𝚃𝙷}^{t h}$ non-zero item of the sequence of variables $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ .

Example

(2, 4, 〈3, 0, 0, 8, 6〉)

The $𝚒𝚝𝚑_𝚙𝚘𝚜_𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚏𝚛𝚘𝚖_0$ constraint holds since 4 corresponds to the position of the 2^th non-zero item of the sequence $30086$ .

Typical

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | > 1

𝚛𝚊𝚗𝚐𝚎

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) > 1

𝚊𝚝𝚕𝚎𝚊𝚜𝚝

(1, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 0)

Symmetry

An occurrence of a value of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛$ that is different from 0 can be replaced by any other value that is also different from 0.

Arg. properties

Suffix-extensible wrt. $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ .

Keywords

constraint type: data constraint.

modelling: table.

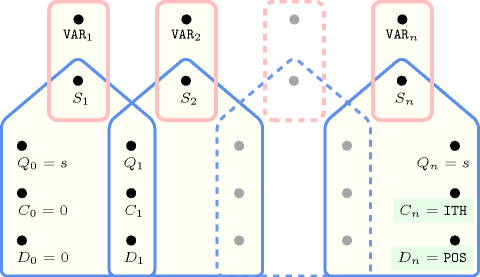
Automaton: Figure 5.203.1 depicts the automaton associated with the $𝚒𝚝𝚑_𝚙𝚘𝚜_𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚏𝚛𝚘𝚖_0$ constraint. To each variable ${𝚅𝙰𝚁}_{i}$ of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ corresponds a 0-1 signature variable $S_{i}$ . The following signature constraint links ${𝚅𝙰𝚁}_{i}$ and $S_{i}$ : ${𝚅𝙰𝚁}_{i} = 0 \Leftrightarrow S_{i}$ .

Figure 5.203.1. Automaton of the $𝚒𝚝𝚑_𝚙𝚘𝚜_𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚏𝚛𝚘𝚖_0$ constraint

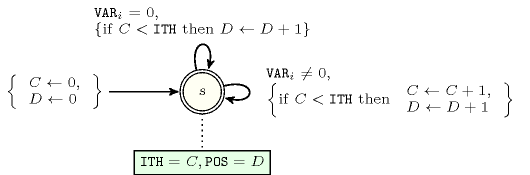
Figure 5.203.2. Hypergraph of the reformulation corresponding to the automaton of the $𝚒𝚝𝚑_𝚙𝚘𝚜_𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚏𝚛𝚘𝚖_0$ constraint