Global Constraint Catalog: Cclause

5.70. clause_or

DESCRIPTION

LINKS

AUTOMATON

Origin

Logic

Constraint

$𝚌𝚕𝚊𝚞𝚜𝚎_𝚘𝚛 (𝙿𝙾𝚂𝚅𝙰𝚁𝚂, 𝙽𝙴𝙶𝚅𝙰𝚁𝚂, 𝚅𝙰𝚁)$

Synonym

$𝚌𝚕𝚊𝚞𝚜𝚎$ .

Arguments

$𝙿𝙾𝚂𝚅𝙰𝚁𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)$
$𝙽𝙴𝙶𝚅𝙰𝚁𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)$
$𝚅𝙰𝚁$	$𝚍𝚟𝚊𝚛$

Restrictions

| 𝙿𝙾𝚂𝚅𝙰𝚁𝚂 | + | 𝙽𝙴𝙶𝚅𝙰𝚁𝚂 | > 0

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝙿𝙾𝚂𝚅𝙰𝚁𝚂, 𝚟𝚊𝚛)

𝙿𝙾𝚂𝚅𝙰𝚁𝚂 . 𝚟𝚊𝚛 \geq 0

𝙿𝙾𝚂𝚅𝙰𝚁𝚂 . 𝚟𝚊𝚛 \leq 1

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝙽𝙴𝙶𝚅𝙰𝚁𝚂, 𝚟𝚊𝚛)

𝙽𝙴𝙶𝚅𝙰𝚁𝚂 . 𝚟𝚊𝚛 \geq 0

𝙽𝙴𝙶𝚅𝙰𝚁𝚂 . 𝚟𝚊𝚛 \leq 1

𝚅𝙰𝚁 \geq 0

𝚅𝙰𝚁 \leq 1

Purpose

Given a first collection of 0-1 variables $𝙿𝙾𝚂𝚅𝙰𝚁𝚂 = U_{1}, U_{2}, \dots, U_{p}$ , a second collection of 0-1 variables $𝙽𝙴𝙶𝚅𝙰𝚁𝚂 = V_{1}, V_{2}, \dots, V_{n}$ , and a variable $𝚅𝙰𝚁$ , enforce $𝚅𝙰𝚁 = (U_{1} \lor U_{2} \lor \dots \lor U_{p}) \lor (\neg V_{1} \lor \neg V_{2} \lor \dots \lor \neg V_{n})$ .

Example

(〈0, 0〉, 〈0〉, 1)

Typical

| 𝙿𝙾𝚂𝚅𝙰𝚁𝚂 | + | 𝙽𝙴𝙶𝚅𝙰𝚁𝚂 | > 1

Symmetries

Items of $𝙿𝙾𝚂𝚅𝙰𝚁𝚂$ are permutable.
Items of $𝙽𝙴𝙶𝚅𝙰𝚁𝚂$ are permutable.

Arg. properties

Extensible wrt. $𝙿𝙾𝚂𝚅𝙰𝚁𝚂$ when $𝚅𝙰𝚁 = 1$ .
Extensible wrt. $𝙽𝙴𝙶𝚅𝙰𝚁𝚂$ when $𝚅𝙰𝚁 = 1$ .

Remark

The $𝚌𝚕𝚊𝚞𝚜𝚎_𝚘𝚛$ constraint is called $𝚌𝚕𝚊𝚞𝚜𝚎$ in Gecode (http://www.gecode.org/).

Systems

reifiedOr in Choco, clause in Choco, clause in Gecode.

Keywords

characteristic of a constraint: automaton, automaton without counters, reified automaton constraint.

constraint network structure: Berge-acyclic constraint network.

constraint type: Boolean constraint.

filtering: arc-consistency.

modelling: disjunction.

Automaton

Figure 5.70.1 depicts the automaton associated with the $𝚌𝚕𝚊𝚞𝚜𝚎_𝚘𝚛$ constraint:

To the argument $𝚅𝙰𝚁$ of the $𝚌𝚕𝚊𝚞𝚜𝚎_𝚘𝚛$ constraint corresponds the first signature variable.
To each variable of the argument $𝙿𝙾𝚂𝚅𝙰𝚁𝚂$ corresponds a signature variable.
Finally, to each variable ${𝚅𝙰𝚁}_{i}$ of the argument $𝙽𝙴𝙶𝚅𝙰𝚁𝚂$ corresponds a signature variable that is the negation of ${𝚅𝙰𝚁}_{i}$ .

Figure 5.70.1. Automaton of the $𝚌𝚕𝚊𝚞𝚜𝚎_𝚘𝚛$ constraint ( ${𝙿𝚅𝙰𝚁}_{i}$ and ${𝙽𝚅𝙰𝚁}_{i}$ respectively denote variables of $𝙿𝙾𝚂𝚅𝙰𝚁𝚂$ and $𝙽𝙴𝙶𝚅𝙰𝚁𝚂$ )

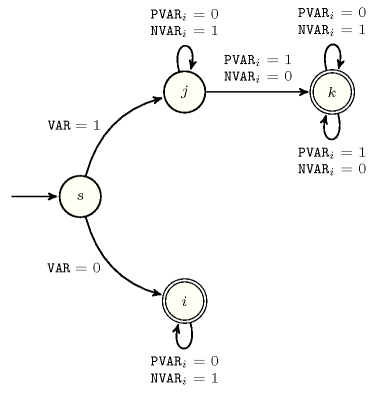
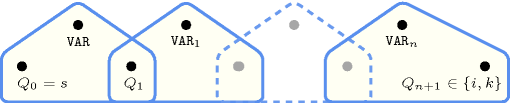
Figure 5.70.2. Hypergraph of the reformulation corresponding to the automaton of the $𝚌𝚕𝚊𝚞𝚜𝚎_𝚘𝚛$ constraint ( ${𝚅𝙰𝚁}_{1}, \dots, {𝚅𝙰𝚁}_{n}$ denotes ${𝙿𝚅𝙰𝚁}_{1}, \dots, {𝙿𝚅𝙰𝚁}_{| 𝙿𝙾𝚂𝚅𝙰𝚁𝚂 |}, 1 - {𝙽𝚅𝙰𝚁}_{1}, \dots, 1 - {𝙽𝚅𝙰𝚁}_{| 𝙽𝙴𝙶𝚅𝙰𝚁𝚂 |}$ )

Global Constraint Catalog

5. Global Constraint Catalogue

5.70. clause_or

Figure 5.70.1. Automaton of the 𝚌𝚕𝚊𝚞𝚜𝚎_𝚘𝚛 constraint (𝙿𝚅𝙰𝚁 i and 𝙽𝚅𝙰𝚁 i respectively denote variables of 𝙿𝙾𝚂𝚅𝙰𝚁𝚂 and 𝙽𝙴𝙶𝚅𝙰𝚁𝚂)

Figure 5.70.1. Automaton of the $𝚌𝚕𝚊𝚞𝚜𝚎_𝚘𝚛$ constraint ( ${𝙿𝚅𝙰𝚁}_{i}$ and ${𝙽𝚅𝙰𝚁}_{i}$ respectively denote variables of $𝙿𝙾𝚂𝚅𝙰𝚁𝚂$ and $𝙽𝙴𝙶𝚅𝙰𝚁𝚂$ )