5.170. graph_crossing
| DESCRIPTION | LINKS | GRAPH |
- Origin
N. Beldiceanu
- Constraint
- Synonyms
, .
- Arguments
- Restrictions
- Purpose
is the number of proper intersections between line segments, where each line segment is an arc of the directed graph defined by the arc linking a node and its unique successor.
- Example
-
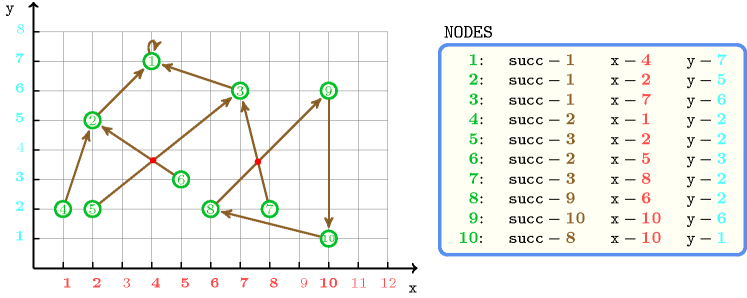
Figure 5.170.1 shows the line segments associated with the collection. One can note the following line segments intersection:
Arcs and cross,
Arcs and cross also.
Consequently, the constraint holds since its first argument is set to 2.
Figure 5.170.1. Illustration of the Example slot: a graph covering with 2 line segments intersections in red ()
- Typical
- Symmetries
Attributes of are permutable w.r.t. permutation (permutation applied to all items).
One and the same constant can be added to the attribute of all items of .
One and the same constant can be added to the attribute of all items of .
- Arg. properties
Functional dependency: determined by .
- Usage
This is a general crossing constraint that can be used in conjunction with one graph covering constraint such as , or . In many practical problems ones want not only to cover a graph with specific patterns but also to avoid too much crossing between the arcs of the final graph.
- Remark
We did not give a specific crossing constraint for each graph covering constraint. We feel that it is better to start first with a more general constraint before going in the specificity of the pattern that is used for covering the graph.
- See also
common keyword: (line segments intersection),
, , (graph constraint,graph partitioning constraint), (line segments intersection).
- Keywords
constraint arguments: pure functional dependency.
constraint type: graph constraint, graph partitioning constraint.
geometry: geometrical constraint, line segments intersection.
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
-
- Graph property(ies)
-
- Graph model
Each node is described by its coordinates and , and by its successor in the final covering. Note that the co-ordinates are initially fixed. We use the arc generator in order to avoid counting twice the same line segment crossing.
Parts (A) and (B) of Figure 5.170.2 respectively show the initial and final graph associated with the Example slot. Since we use the graph property, the arcs of the final graph are stressed in bold. Each arc of the final graph corresponds to a proper intersection between two line segments.
Figure 5.170.2. Initial and final graph of the constraint
(a) 
(b)