Global Constraint Catalog: Cproduct

5.327. product_ctr

DESCRIPTION

LINKS

GRAPH

Origin

Arithmetic constraint.

Constraint

$𝚙𝚛𝚘𝚍𝚞𝚌𝚝_𝚌𝚝𝚛 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝙲𝚃𝚁, 𝚅𝙰𝚁)$

Arguments

$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)$
$𝙲𝚃𝚁$	$𝚊𝚝𝚘𝚖$
$𝚅𝙰𝚁$	$𝚍𝚟𝚊𝚛$

Restrictions

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚟𝚊𝚛)

𝙲𝚃𝚁 \in [=, \neq, <, \geq, >, \leq]

Purpose

Constraint the product of a set of domain variables. More precisely, let $𝙿$ denote the product of the variables of the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ collection. Enforce the following constraint to hold: $𝙿 𝙲𝚃𝚁 𝚅𝙰𝚁$ .

Example

(〈2, 1, 4〉, =, 8)

The $𝚙𝚛𝚘𝚍𝚞𝚌𝚝_𝚌𝚝𝚛$ constraint holds since its last argument $𝚅𝙰𝚁 = 8$ is equal (i.e., $𝙲𝚃𝚁$ is set to $=$ ) to $2 \cdot 1 \cdot 4$ .

Typical

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | > 1

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | < 10

𝚛𝚊𝚗𝚐𝚎

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) > 1

𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛 \neq 0

𝙲𝚃𝚁 \in [=, <, \geq, >, \leq]

𝚅𝙰𝚁 \neq 0

Symmetry

Items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ are permutable.

Arg. properties

Contractible wrt. $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ when $𝙲𝚃𝚁 \in [<, \leq]$ and $𝚖𝚒𝚗𝚟𝚊𝚕 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) > 0$ .
Aggregate: $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 (𝚞𝚗𝚒𝚘𝚗)$ , $𝙲𝚃𝚁 (𝚒𝚍)$ , $𝚅𝙰𝚁 (*)$ when $𝙲𝚃𝚁 \in [=]$ .

Used in

$𝚌𝚞𝚖𝚞𝚕𝚊𝚝𝚒𝚟𝚎_𝚙𝚛𝚘𝚍𝚞𝚌𝚝$ .

Keywords

characteristic of a constraint: product.

constraint type: arithmetic constraint.

Arc input(s)

$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$

Arc generator

𝑆𝐸𝐿𝐹

\mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜)

Arc arity

Arc constraint(s)

𝚃𝚁𝚄𝙴

Graph property(ies)

𝐏𝐑𝐎𝐃

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚟𝚊𝚛) 𝙲𝚃𝚁 𝚅𝙰𝚁

Graph model

Since we want to keep all the vertices of the initial graph we use the $𝑆𝐸𝐿𝐹$ arc generator together with the $𝚃𝚁𝚄𝙴$ arc constraint. This predefined arc constraint always holds.

Parts (A) and (B) of Figure 5.327.1 respectively show the initial and final graph associated with the Example slot. Since we use the $𝚃𝚁𝚄𝙴$ arc constraint both graphs are identical.

Figure 5.327.1. Initial and final graph of the $𝚙𝚛𝚘𝚍𝚞𝚌𝚝_𝚌𝚝𝚛$ constraint


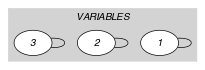
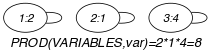
(a)	(b)

Global Constraint Catalog

5. Global Constraint Catalogue

5.327. product_ctr

Figure 5.327.1. Initial and final graph of the 𝚙𝚛𝚘𝚍𝚞𝚌𝚝_𝚌𝚝𝚛 constraint

Figure 5.327.1. Initial and final graph of the $𝚙𝚛𝚘𝚍𝚞𝚌𝚝_𝚌𝚝𝚛$ constraint