5.345. shift
| DESCRIPTION | LINKS | GRAPH |
- Origin
N. Beldiceanu
- Constraint
- Arguments
- Restrictions
- Purpose
The difference between the end of the last task of a shift and the origin of the first task of a shift should not exceed the quantity . Two tasks and belong to the same shift if at least one of the following conditions is true:
Task starts after the end of task at a distance that is less than or equal to the quantity ,
Task starts after the end of task at a distance that is less than or equal to the quantity .
Task overlaps task .
- Example
-
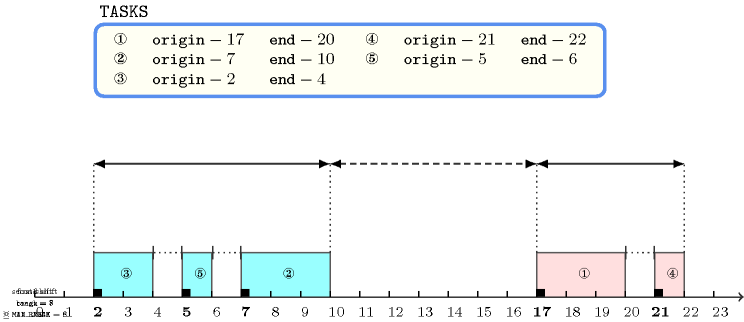
Figure 5.345.1 represents the different tasks of the example. Each task is drawn as a rectangle with its corresponding attribute in the middle. We indicate the distance between two consecutive tasks of a same shift and note that it is less than or equal to . Since each shift has a range that is less than or equal to , the constraint holds (the range of a shift is the difference between the end of the last task of the shift and the origin of the first task of the shift).
Figure 5.345.1. The two shifts of the Example slot
- Typical
- Symmetries
Items of are permutable.
One and the same constant can be added to the attribute of all items of .
- Usage
The shift constraint can be used in machine scheduling problems where one has to shut down a machine for maintenance purpose after a given maximum utilisation of that machine. In this case the parameter indicates the maximum possible utilisation of the machine before maintenance, while the parameter gives the minimum time needed for maintenance.
The shift constraint can also be used for timetabling problems where the rest period of a person can move in time. In this case indicates the maximum possible working time for a person, while specifies the minimum length of the break that follows a working time period.
- See also
- Keywords
constraint type: scheduling constraint, timetabling constraint, temporal constraint.
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
-
- Graph property(ies)
-
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
- Sets
-
- Constraint(s) on sets
- Graph model
The first graph constraint forces the following two constraints between the attributes of each task:
The end of a task should not be situated before its start,
The duration of a task should not be greater than the parameter.
The second graph constraint decomposes the final graph in connected components where each component corresponds to a given shift. Finally, the Constraint(s) on sets slot restricts the stretch of each shift.
Parts (A) and (B) of Figure 5.345.2 respectively show the initial and final graph associated with the second graph constraint of the Example slot. Since we use the set generator we show the two connected components of the final graph. They respectively correspond to the two shifts that are displayed in Figure 5.345.1.
Figure 5.345.2. Initial and final graph of the constraint
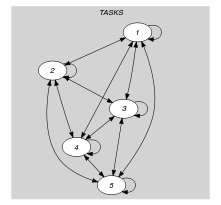
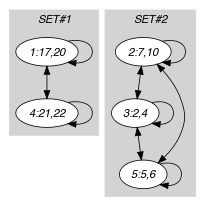
(a) (b) - Signature
Consider the first graph constraint. Since we use the arc generator on the collection the maximum number of arcs of the final graph is equal to . Therefore we can rewrite the graph property to and simplify to .