Global Constraint Catalog: Celements

5.146. elements

DESCRIPTION

LINKS

GRAPH

Origin

Derived from $𝚎𝚕𝚎𝚖𝚎𝚗𝚝$ .

Constraint

$𝚎𝚕𝚎𝚖𝚎𝚗𝚝𝚜 (𝙸𝚃𝙴𝙼𝚂, 𝚃𝙰𝙱𝙻𝙴)$

Arguments

$𝙸𝚃𝙴𝙼𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚒𝚗𝚍𝚎𝚡 - 𝚍𝚟𝚊𝚛, 𝚟𝚊𝚕𝚞𝚎 - 𝚍𝚟𝚊𝚛)$
$𝚃𝙰𝙱𝙻𝙴$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚒𝚗𝚍𝚎𝚡 - 𝚒𝚗𝚝, 𝚟𝚊𝚕𝚞𝚎 - 𝚍𝚟𝚊𝚛)$

Restrictions

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝙸𝚃𝙴𝙼𝚂, [𝚒𝚗𝚍𝚎𝚡, 𝚟𝚊𝚕𝚞𝚎])

𝙸𝚃𝙴𝙼𝚂 . 𝚒𝚗𝚍𝚎𝚡 \geq 1

𝙸𝚃𝙴𝙼𝚂 . 𝚒𝚗𝚍𝚎𝚡 \leq | 𝚃𝙰𝙱𝙻𝙴 |

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚃𝙰𝙱𝙻𝙴, [𝚒𝚗𝚍𝚎𝚡, 𝚟𝚊𝚕𝚞𝚎])

𝚃𝙰𝙱𝙻𝙴 . 𝚒𝚗𝚍𝚎𝚡 \geq 1

𝚃𝙰𝙱𝙻𝙴 . 𝚒𝚗𝚍𝚎𝚡 \leq | 𝚃𝙰𝙱𝙻𝙴 |

𝚍𝚒𝚜𝚝𝚒𝚗𝚌𝚝

(𝚃𝙰𝙱𝙻𝙴, 𝚒𝚗𝚍𝚎𝚡)

Purpose

All the items of $𝙸𝚃𝙴𝙼𝚂$ should be equal to one of the entries of the table $𝚃𝙰𝙱𝙻𝙴$ .

Example

(\begin{matrix} 〈𝚒𝚗𝚍𝚎𝚡 - 4 𝚟𝚊𝚕𝚞𝚎 - 9, 𝚒𝚗𝚍𝚎𝚡 - 1 𝚟𝚊𝚕𝚞𝚎 - 6〉, \\ 〈\begin{matrix} 𝚒𝚗𝚍𝚎𝚡 - 1 & 𝚟𝚊𝚕𝚞𝚎 - 6, \\ 𝚒𝚗𝚍𝚎𝚡 - 2 & 𝚟𝚊𝚕𝚞𝚎 - 9, \\ 𝚒𝚗𝚍𝚎𝚡 - 3 & 𝚟𝚊𝚕𝚞𝚎 - 2, \\ 𝚒𝚗𝚍𝚎𝚡 - 4 & 𝚟𝚊𝚕𝚞𝚎 - 9 \end{matrix}〉 \end{matrix})

The $𝚎𝚕𝚎𝚖𝚎𝚗𝚝𝚜$ constraint holds since each item of its first argument $𝙸𝚃𝙴𝙼𝚂$ corresponds to an item of the $𝚃𝙰𝙱𝙻𝙴$ collection: the first item $〈 𝚒𝚗𝚍𝚎𝚡 - 4 𝚟𝚊𝚕𝚞𝚎 - 9 〉$ of $𝙸𝚃𝙴𝙼𝚂$ corresponds to the fourth item of $𝚃𝙰𝙱𝙻𝙴$ , while the second item $〈 𝚒𝚗𝚍𝚎𝚡 - 1 𝚟𝚊𝚕𝚞𝚎 - 6 〉$ of $𝙸𝚃𝙴𝙼𝚂$ corresponds to the first item of $𝚃𝙰𝙱𝙻𝙴$ .

Typical

| 𝙸𝚃𝙴𝙼𝚂 | > 1

𝚛𝚊𝚗𝚐𝚎

(𝙸𝚃𝙴𝙼𝚂 . 𝚒𝚗𝚍𝚎𝚡) > 1

| 𝚃𝙰𝙱𝙻𝙴 | > 1

𝚛𝚊𝚗𝚐𝚎

(𝚃𝙰𝙱𝙻𝙴 . 𝚟𝚊𝚕𝚞𝚎) > 1

Symmetries

Items of $𝙸𝚃𝙴𝙼𝚂$ are permutable.
Items of $𝚃𝙰𝙱𝙻𝙴$ are permutable.
All occurrences of two distinct values in $𝙸𝚃𝙴𝙼𝚂 . 𝚟𝚊𝚕𝚞𝚎$ or $𝚃𝙰𝙱𝙻𝙴 . 𝚟𝚊𝚕𝚞𝚎$ can be swapped; all occurrences of a value in $𝙸𝚃𝙴𝙼𝚂 . 𝚟𝚊𝚕𝚞𝚎$ or $𝚃𝙰𝙱𝙻𝙴 . 𝚟𝚊𝚕𝚞𝚎$ can be renamed to any unused value.

Arg. properties

Functional dependency: $𝙸𝚃𝙴𝙼𝚂 . 𝚟𝚊𝚕𝚞𝚎$ determined by $𝙸𝚃𝙴𝙼𝚂 . 𝚒𝚗𝚍𝚎𝚡$ and $𝚃𝙰𝙱𝙻𝙴$ .

Usage

Used for replacing several $𝚎𝚕𝚎𝚖𝚎𝚗𝚝$ constraints sharing exactly the same table by a single constraint.

Reformulation

The $𝚎𝚕𝚎𝚖𝚎𝚗𝚝𝚜$ $(〈 𝚒𝚗𝚍𝚎𝚡 - I_{1} 𝚟𝚊𝚕𝚞𝚎 - V_{1}, 𝚒𝚗𝚍𝚎𝚡 - I_{2} 𝚟𝚊𝚕𝚞𝚎 - V_{2}, \dots, 𝚒𝚗𝚍𝚎𝚡 - I_{| 𝙸𝚃𝙴𝙼𝚂 |} 𝚟𝚊𝚕𝚞𝚎 - V_{| 𝙸𝚃𝙴𝙼𝚂 |} 〉, 𝚃𝙰𝙱𝙻𝙴)$ constraint can be expressed in term of a conjunction of $| 𝙸𝚃𝙴𝙼𝚂 |$ $𝚎𝚕𝚎𝚖$ constraints of the form:

$𝚎𝚕𝚎𝚖$ $(〈 𝚒𝚗𝚍𝚎𝚡 - I_{1} 𝚟𝚊𝚕𝚞𝚎 - V_{1} 〉, 𝚃𝙰𝙱𝙻𝙴)$ ,

$𝚎𝚕𝚎𝚖$ $(〈 𝚒𝚗𝚍𝚎𝚡 - I_{2} 𝚟𝚊𝚕𝚞𝚎 - V_{2} 〉, 𝚃𝙰𝙱𝙻𝙴)$ ,

$\dots$

$𝚎𝚕𝚎𝚖$ $(〈 𝚒𝚗𝚍𝚎𝚡 - I_{| 𝙸𝚃𝙴𝙼𝚂 |} 𝚟𝚊𝚕𝚞𝚎 - V_{| 𝙸𝚃𝙴𝙼𝚂 |} 〉, 𝚃𝙰𝙱𝙻𝙴)$ .

part of system of constraints: $𝚎𝚕𝚎𝚖$ , $𝚎𝚕𝚎𝚖𝚎𝚗𝚝$ .

Keywords

constraint arguments: pure functional dependency.

constraint type: data constraint, system of constraints.

filtering: arc-consistency.

modelling: table, shared table, functional dependency.

Cond. implications

$𝚎𝚕𝚎𝚖𝚎𝚗𝚝𝚜 (𝙸𝚃𝙴𝙼𝚂, 𝚃𝙰𝙱𝙻𝙴)$

with $𝚍𝚒𝚜𝚝𝚒𝚗𝚌𝚝$ $(𝙸𝚃𝙴𝙼𝚂, 𝚒𝚗𝚍𝚎𝚡)$

and $𝚃𝙰𝙱𝙻𝙴 . 𝚟𝚊𝚕𝚞𝚎 \geq 0$

implies $𝚋𝚒𝚗_𝚙𝚊𝚌𝚔𝚒𝚗𝚐_𝚌𝚊𝚙𝚊$ $(𝚃𝙰𝙱𝙻𝙴, 𝙸𝚃𝙴𝙼𝚂)$ .

Arc input(s)

$𝙸𝚃𝙴𝙼𝚂$ $𝚃𝙰𝙱𝙻𝙴$

Arc generator

𝑃𝑅𝑂𝐷𝑈𝐶𝑇

\mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚒𝚝𝚎𝚖𝚜, 𝚝𝚊𝚋𝚕𝚎)

Arc arity

Arc constraint(s)

• 𝚒𝚝𝚎𝚖𝚜 . 𝚒𝚗𝚍𝚎𝚡 = 𝚝𝚊𝚋𝚕𝚎 . 𝚒𝚗𝚍𝚎𝚡

• 𝚒𝚝𝚎𝚖𝚜 . 𝚟𝚊𝚕𝚞𝚎 = 𝚝𝚊𝚋𝚕𝚎 . 𝚟𝚊𝚕𝚞𝚎

Graph property(ies)

𝐍𝐀𝐑𝐂

= | 𝙸𝚃𝙴𝙼𝚂 |

Graph model

Parts (A) and (B) of Figure 5.146.1 respectively show the initial and final graph associated with the Example slot. Since we use the $𝐍𝐀𝐑𝐂$ graph property, the arcs of the final graph are stressed in bold.

Figure 5.146.1. Initial and final graph of the $𝚎𝚕𝚎𝚖𝚎𝚗𝚝𝚜$ constraint


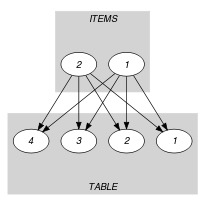
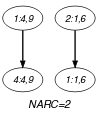
(a)	(b)

Signature

Since all the $𝚒𝚗𝚍𝚎𝚡$ attributes of $𝚃𝙰𝙱𝙻𝙴$ collection are distinct and because of the first condition $𝚒𝚝𝚎𝚖𝚜 . 𝚒𝚗𝚍𝚎𝚡 = 𝚝𝚊𝚋𝚕𝚎 . 𝚒𝚗𝚍𝚎𝚡$ of the arc constraint, a source vertex of the final graph can have at most one successor. Therefore $| 𝙸𝚃𝙴𝙼𝚂 |$ is the maximum number of arcs of the final graph and we can rewrite $𝐍𝐀𝐑𝐂 = | 𝙸𝚃𝙴𝙼𝚂 |$ to $𝐍𝐀𝐑𝐂 \geq | 𝙸𝚃𝙴𝙼𝚂 |$ . So we can simplify $\underset{̲}{\bar{𝐍𝐀𝐑𝐂}}$ to $\bar{𝐍𝐀𝐑𝐂}$ .

Global Constraint Catalog

5. Global Constraint Catalogue

5.146. elements

Figure 5.146.1. Initial and final graph of the 𝚎𝚕𝚎𝚖𝚎𝚗𝚝𝚜 constraint

Figure 5.146.1. Initial and final graph of the $𝚎𝚕𝚎𝚖𝚎𝚗𝚝𝚜$ constraint