Global Constraint Catalog: Camong

5.27. among_modulo

DESCRIPTION

LINKS

GRAPH

AUTOMATON

Origin

Derived from $𝚊𝚖𝚘𝚗𝚐$ .

Constraint

$𝚊𝚖𝚘𝚗𝚐_𝚖𝚘𝚍𝚞𝚕𝚘 (𝙽𝚅𝙰𝚁, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚁𝙴𝙼𝙰𝙸𝙽𝙳𝙴𝚁, 𝚀𝚄𝙾𝚃𝙸𝙴𝙽𝚃)$

Arguments

$𝙽𝚅𝙰𝚁$	$𝚍𝚟𝚊𝚛$
$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)$
$𝚁𝙴𝙼𝙰𝙸𝙽𝙳𝙴𝚁$	$𝚒𝚗𝚝$
$𝚀𝚄𝙾𝚃𝙸𝙴𝙽𝚃$	$𝚒𝚗𝚝$

Restrictions

𝙽𝚅𝙰𝚁 \geq 0

𝙽𝚅𝙰𝚁 \leq | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚟𝚊𝚛)

𝚁𝙴𝙼𝙰𝙸𝙽𝙳𝙴𝚁 \geq 0

𝚁𝙴𝙼𝙰𝙸𝙽𝙳𝙴𝚁 < 𝚀𝚄𝙾𝚃𝙸𝙴𝙽𝚃

𝚀𝚄𝙾𝚃𝙸𝙴𝙽𝚃 > 0

Purpose

$𝙽𝚅𝙰𝚁$ is the number of variables of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ taking a value that is congruent to $𝚁𝙴𝙼𝙰𝙸𝙽𝙳𝙴𝚁$ modulo $𝚀𝚄𝙾𝚃𝙸𝙴𝙽𝚃$ .

Example

(3, 〈4, 5, 8, 4, 1〉, 0, 2)

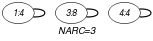
In this example $𝚁𝙴𝙼𝙰𝙸𝙽𝙳𝙴𝚁 = 0$ and $𝚀𝚄𝙾𝚃𝙸𝙴𝙽𝚃 = 2$ specifies that we count the number of even values taken by the different variables. As a consequence the $𝚊𝚖𝚘𝚗𝚐_𝚖𝚘𝚍𝚞𝚕𝚘$ constraint holds since exactly 3 values of the collection $〈 4, 5, 8, 4, 1 〉$ are even.

Typical

𝙽𝚅𝙰𝚁 > 0

𝙽𝚅𝙰𝚁 < | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | > 1

𝚀𝚄𝙾𝚃𝙸𝙴𝙽𝚃 > 1

𝚀𝚄𝙾𝚃𝙸𝙴𝙽𝚃 <

𝚖𝚊𝚡𝚟𝚊𝚕

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛)

Symmetries

Items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ are permutable.
An occurrence of a value $u$ of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛$ such that $u \mod 𝚀𝚄𝙾𝚃𝙸𝙴𝙽𝚃 = 𝚁𝙴𝙼𝙰𝙸𝙽𝙳𝙴𝚁$ (resp. $u \mod 𝚀𝚄𝙾𝚃𝙸𝙴𝙽𝚃 \neq 𝚁𝙴𝙼𝙰𝙸𝙽𝙳𝙴𝚁$ ) can be replaced by any other value $v$ such that $v \mod 𝚀𝚄𝙾𝚃𝙸𝙴𝙽𝚃 = 𝚁𝙴𝙼𝙰𝙸𝙽𝙳𝙴𝚁$ (resp. $u \mod 𝚀𝚄𝙾𝚃𝙸𝙴𝙽𝚃 \neq 𝚁𝙴𝙼𝙰𝙸𝙽𝙳𝙴𝚁$ ).

Arg. properties

Functional dependency: $𝙽𝚅𝙰𝚁$ determined by $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ , $𝚁𝙴𝙼𝙰𝙸𝙽𝙳𝙴𝚁$ and $𝚀𝚄𝙾𝚃𝙸𝙴𝙽𝚃$ .
Contractible wrt. $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ when $𝙽𝚅𝙰𝚁 = 0$ .
Contractible wrt. $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ when $𝙽𝚅𝙰𝚁 = | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |$ .
Aggregate: $𝙽𝚅𝙰𝚁 (+)$ , $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 (𝚞𝚗𝚒𝚘𝚗)$ , $𝚁𝙴𝙼𝙰𝙸𝙽𝙳𝙴𝚁 (𝚒𝚍)$ , $𝚀𝚄𝙾𝚃𝙸𝙴𝙽𝚃 (𝚒𝚍)$ .

Remark

By giving explicitly all values $v$ that satisfy the equality $v \mod 𝚀𝚄𝙾𝚃𝙸𝙴𝙽𝚃 = 𝚁𝙴𝙼𝙰𝙸𝙽𝙳𝙴𝚁$ , the $𝚊𝚖𝚘𝚗𝚐_𝚖𝚘𝚍𝚞𝚕𝚘$ constraint can be modelled with the $𝚊𝚖𝚘𝚗𝚐$ constraint. However the $𝚊𝚖𝚘𝚗𝚐_𝚖𝚘𝚍𝚞𝚕𝚘$ constraint provides a more compact form.

See also

generalisation: $𝚊𝚖𝚘𝚗𝚐$ (list of $𝚟𝚊𝚕𝚞𝚎𝚜$ $𝚟$ such that $𝚟 \mod 𝚀𝚄𝙾𝚃𝙸𝙴𝙽𝚃$ = $𝚁𝙴𝙼𝙰𝙸𝙽𝙳𝙴𝚁$ replaced by list of $𝚟𝚊𝚕𝚞𝚎𝚜$ ).

Keywords

characteristic of a constraint: modulo, automaton, automaton with counters.

constraint arguments: pure functional dependency.

constraint network structure: alpha-acyclic constraint network(2).

constraint type: value constraint, counting constraint.

filtering: arc-consistency.

modelling: functional dependency.

Arc input(s)

$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$

Arc generator

𝑆𝐸𝐿𝐹

\mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜)

Arc arity

Arc constraint(s)

𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 . 𝚟𝚊𝚛 \mod 𝚀𝚄𝙾𝚃𝙸𝙴𝙽𝚃 = 𝚁𝙴𝙼𝙰𝙸𝙽𝙳𝙴𝚁

Graph property(ies)

𝐍𝐀𝐑𝐂

= 𝙽𝚅𝙰𝚁

Graph model

The arc constraint corresponds to a unary constraint. For this reason we employ the $𝑆𝐸𝐿𝐹$ arc generator in order to produce a graph with a single loop on each vertex.

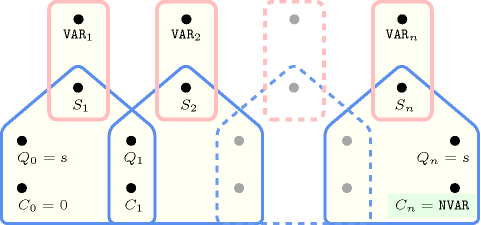
Parts (A) and (B) of Figure 5.27.1 respectively show the initial and final graph associated with the Example slot. Since we use the $𝐍𝐀𝐑𝐂$ graph property, the loops of the final graph are stressed in bold.

Figure 5.27.1. Initial and final graph of the $𝚊𝚖𝚘𝚗𝚐_𝚖𝚘𝚍𝚞𝚕𝚘$ constraint


(a)	(b)

Automaton: Figure 5.27.2 depicts the automaton associated with the $𝚊𝚖𝚘𝚗𝚐_𝚖𝚘𝚍𝚞𝚕𝚘$ constraint. To each variable ${𝚅𝙰𝚁}_{i}$ of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ corresponds a 0-1 signature variable $S_{i}$ . The following signature constraint links ${𝚅𝙰𝚁}_{i}$ and $S_{i}$ : ${𝚅𝙰𝚁}_{i} \mod 𝚀𝚄𝙾𝚃𝙸𝙴𝙽𝚃 = 𝚁𝙴𝙼𝙰𝙸𝙽𝙳𝙴𝚁 \Leftrightarrow S_{i}$ .

Figure 5.27.2. Automaton of the $𝚊𝚖𝚘𝚗𝚐_𝚖𝚘𝚍𝚞𝚕𝚘$ constraint

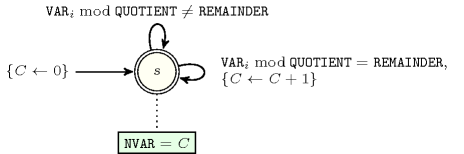
Figure 5.27.3. Hypergraph of the reformulation corresponding to the automaton (with one counter) of the $𝚊𝚖𝚘𝚗𝚐_𝚖𝚘𝚍𝚞𝚕𝚘$ constraint: since all states variables $Q_{0}, Q_{1}, \dots, Q_{n}$ are fixed to the unique state $s$ of the automaton, the transitions constraints share only the counter variable $C$ and the constraint network is Berge-acyclic

Global Constraint Catalog

5. Global Constraint Catalogue

5.27. among_modulo

Figure 5.27.1. Initial and final graph of the $𝚊𝚖𝚘𝚗𝚐_𝚖𝚘𝚍𝚞𝚕𝚘$ constraint

Figure 5.27.2. Automaton of the $𝚊𝚖𝚘𝚗𝚐_𝚖𝚘𝚍𝚞𝚕𝚘$ constraint

Global Constraint Catalog

5. Global Constraint Catalogue

5.27. among_modulo

Figure 5.27.1. Initial and final graph of the 𝚊𝚖𝚘𝚗𝚐_𝚖𝚘𝚍𝚞𝚕𝚘 constraint

Figure 5.27.2. Automaton of the 𝚊𝚖𝚘𝚗𝚐_𝚖𝚘𝚍𝚞𝚕𝚘 constraint

Figure 5.27.1. Initial and final graph of the $𝚊𝚖𝚘𝚗𝚐_𝚖𝚘𝚍𝚞𝚕𝚘$ constraint

Figure 5.27.2. Automaton of the $𝚊𝚖𝚘𝚗𝚐_𝚖𝚘𝚍𝚞𝚕𝚘$ constraint