Global Constraint Catalog: Cordered_atleast

5.306. ordered_atleast_nvector

DESCRIPTION

LINKS

GRAPH

Origin

Conjoin $𝚊𝚝𝚕𝚎𝚊𝚜𝚝_𝚗𝚟𝚎𝚌𝚝𝚘𝚛$ and $𝚕𝚎𝚡_𝚌𝚑𝚊𝚒𝚗_𝚕𝚎𝚜𝚜𝚎𝚚$ .

Constraint

$𝚘𝚛𝚍𝚎𝚛𝚎𝚍_𝚊𝚝𝚕𝚎𝚊𝚜𝚝_𝚗𝚟𝚎𝚌𝚝𝚘𝚛 (𝙽𝚅𝙴𝙲, 𝚅𝙴𝙲𝚃𝙾𝚁𝚂)$

Synonyms

$𝚘𝚛𝚍𝚎𝚛𝚎𝚍_𝚊𝚝𝚕𝚎𝚊𝚜𝚝_𝚗𝚟𝚎𝚌𝚝𝚘𝚛𝚜$ , $𝚘𝚛𝚍𝚎𝚛𝚎𝚍_𝚊𝚝𝚕𝚎𝚊𝚜𝚝_𝚗𝚙𝚘𝚒𝚗𝚝$ , $𝚘𝚛𝚍𝚎𝚛𝚎𝚍_𝚊𝚝𝚕𝚎𝚊𝚜𝚝_𝚗𝚙𝚘𝚒𝚗𝚝𝚜$ .

Type

𝚅𝙴𝙲𝚃𝙾𝚁

𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)

Arguments

$𝙽𝚅𝙴𝙲$	$𝚍𝚟𝚊𝚛$
$𝚅𝙴𝙲𝚃𝙾𝚁𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚎𝚌 - 𝚅𝙴𝙲𝚃𝙾𝚁)$

Restrictions

| 𝚅𝙴𝙲𝚃𝙾𝚁 | \geq 1

𝙽𝚅𝙴𝙲 \geq 0

𝙽𝚅𝙴𝙲 \leq | 𝚅𝙴𝙲𝚃𝙾𝚁𝚂 |

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙴𝙲𝚃𝙾𝚁𝚂, 𝚟𝚎𝚌)

𝚜𝚊𝚖𝚎_𝚜𝚒𝚣𝚎

(𝚅𝙴𝙲𝚃𝙾𝚁𝚂, 𝚟𝚎𝚌)

Purpose

Enforces the following two conditions:

The number of distinct tuples of values taken by the vectors of the collection $𝚅𝙴𝙲𝚃𝙾𝚁𝚂$ is greater than or equal to $𝙽𝚅𝙴𝙲$ . Two tuples of values $〈 A_{1}, A_{2}, \dots, A_{m} 〉$ and $〈 B_{1}, B_{2}, \dots, B_{m} 〉$ are $d i s t i n c t$ if and only if there exist an integer $i \in [1, m]$ such that $A_{i} \neq B_{i}$ .
For each pair of consecutive vectors ${𝚅𝙴𝙲𝚃𝙾𝚁}_{i}$ and ${𝚅𝙴𝙲𝚃𝙾𝚁}_{i + 1}$ of the $𝚅𝙴𝙲𝚃𝙾𝚁𝚂$ collection we have that ${𝚅𝙴𝙲𝚃𝙾𝚁}_{i}$ is lexicographically less than or equal to ${𝚅𝙴𝙲𝚃𝙾𝚁}_{i + 1}$ . Given two vectors, $\vec{X}$ and $\vec{Y}$ of $n$ components, $〈 X_{0}, \dots, X_{n - 1} 〉$ and $〈 Y_{0}, \dots, Y_{n - 1} 〉$ , $\vec{X}$ is lexicographically less than or equal to $\vec{Y}$ if and only if $n = 0$ or $X_{0} < Y_{0}$ or $X_{0} = Y_{0}$ and $〈 X_{1}, \dots, X_{n - 1} 〉$ is lexicographically less than or equal to $〈 Y_{1}, \dots, Y_{n - 1} 〉$ .

Example

(\begin{matrix} 2, 〈\begin{matrix} 𝚟𝚎𝚌 - 〈5, 6〉, \\ 𝚟𝚎𝚌 - 〈5, 6〉, \\ 𝚟𝚎𝚌 - 〈5, 6〉, \\ 𝚟𝚎𝚌 - 〈9, 3〉, \\ 𝚟𝚎𝚌 - 〈9, 4〉 \end{matrix}〉 \end{matrix})

The $𝚘𝚛𝚍𝚎𝚛𝚎𝚍_𝚊𝚝𝚕𝚎𝚊𝚜𝚝_𝚗𝚟𝚎𝚌𝚝𝚘𝚛$ constraint holds since:

The collection $𝚅𝙴𝙲𝚃𝙾𝚁𝚂$ involves at least 2 distinct tuples of values (i.e., in fact the 3 distinct tuples $〈 5, 6 〉$ , $〈 9, 3 〉$ and $〈 9, 4 〉$ ).
The vectors of the collection $𝚅𝙴𝙲𝚃𝙾𝚁𝚂$ are sorted in increasing lexicographical order.

Typical

| 𝚅𝙴𝙲𝚃𝙾𝚁 | > 1

𝙽𝚅𝙴𝙲 > 0

𝙽𝚅𝙴𝙲 < | 𝚅𝙴𝙲𝚃𝙾𝚁𝚂 |

| 𝚅𝙴𝙲𝚃𝙾𝚁𝚂 | > 1

Symmetry

$𝙽𝚅𝙴𝙲$ can be decreased to any value $\geq 0$ .

Reformulation

The $𝚘𝚛𝚍𝚎𝚛𝚎𝚍_𝚊𝚝𝚕𝚎𝚊𝚜𝚝_𝚗𝚟𝚎𝚌𝚝𝚘𝚛$ constraint can be reformulated as a conjunction of a $𝚊𝚝𝚕𝚎𝚊𝚜𝚝_𝚗𝚟𝚎𝚌𝚝𝚘𝚛$ and a $𝚕𝚎𝚡_𝚌𝚑𝚊𝚒𝚗_𝚕𝚎𝚜𝚜𝚎𝚚$ constraints.

comparison swapped: $𝚘𝚛𝚍𝚎𝚛𝚎𝚍_𝚊𝚝𝚖𝚘𝚜𝚝_𝚗𝚟𝚎𝚌𝚝𝚘𝚛$ .

implied by: $𝚘𝚛𝚍𝚎𝚛𝚎𝚍_𝚗𝚟𝚎𝚌𝚝𝚘𝚛$ ( $\geq 𝙽𝚅𝙴𝙲$ replaced by $= 𝙽𝚅𝙴𝙲$ ).

implies: $𝚊𝚝𝚕𝚎𝚊𝚜𝚝_𝚗𝚟𝚎𝚌𝚝𝚘𝚛$ , $𝚕𝚎𝚡_𝚌𝚑𝚊𝚒𝚗_𝚕𝚎𝚜𝚜𝚎𝚚$ ( $𝙽𝚅𝙴𝙲$ of constraint $𝚘𝚛𝚍𝚎𝚛𝚎𝚍_𝚊𝚝𝚕𝚎𝚊𝚜𝚝_𝚗𝚟𝚎𝚌𝚝𝚘𝚛$ removed).

used in graph description: $𝚕𝚎𝚡_𝚕𝚎𝚜𝚜$ , $𝚕𝚎𝚡_𝚕𝚎𝚜𝚜𝚎𝚚$ .

Keywords

characteristic of a constraint: vector.

constraint type: counting constraint, order constraint.

symmetry: symmetry.

Arc input(s)

$𝚅𝙴𝙲𝚃𝙾𝚁𝚂$

Arc generator

𝑃𝐴𝑇𝐻

\mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚎𝚌𝚝𝚘𝚛𝚜 1, 𝚟𝚎𝚌𝚝𝚘𝚛𝚜 2)

Arc arity

Arc constraint(s)

𝚕𝚎𝚡_𝚕𝚎𝚜𝚜𝚎𝚚

(𝚟𝚎𝚌𝚝𝚘𝚛𝚜 1 . 𝚟𝚎𝚌, 𝚟𝚎𝚌𝚝𝚘𝚛𝚜 2 . 𝚟𝚎𝚌)

Graph property(ies)

𝐍𝐀𝐑𝐂

= | 𝚅𝙴𝙲𝚃𝙾𝚁𝚂 | - 1

Arc input(s)

$𝚅𝙴𝙲𝚃𝙾𝚁𝚂$

Arc generator

𝑃𝐴𝑇𝐻

\mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚎𝚌𝚝𝚘𝚛𝚜 1, 𝚟𝚎𝚌𝚝𝚘𝚛𝚜 2)

Arc arity

Arc constraint(s)

𝚕𝚎𝚡_𝚕𝚎𝚜𝚜

(𝚟𝚎𝚌𝚝𝚘𝚛𝚜 1 . 𝚟𝚎𝚌, 𝚟𝚎𝚌𝚝𝚘𝚛𝚜 2 . 𝚟𝚎𝚌)

Graph property(ies)

𝐍𝐂𝐂

\geq 𝙽𝚅𝙴𝙲

Graph model

Parts (A) and (B) of Figure 5.306.1 respectively show the initial and final graph of the second graph constraint associated with the Example slot. Since we use the $𝐍𝐂𝐂$ graph property in this second graph constraint, we show the different connected components of the final graph. Each strongly connected component corresponds to a tuple of values that is assigned to some vectors of the $𝚅𝙴𝙲𝚃𝙾𝚁𝚂$ collection. The 3 following tuple of values $〈 5, 6 〉$ , $〈 9, 3 〉$ and $〈 9, 4 〉$ are used by the vectors of the $𝚅𝙴𝙲𝚃𝙾𝚁𝚂$ collection.

Figure 5.306.1. Initial and final graph of the $𝚘𝚛𝚍𝚎𝚛𝚎𝚍_𝚊𝚝𝚕𝚎𝚊𝚜𝚝_𝚗𝚟𝚎𝚌𝚝𝚘𝚛$ constraint


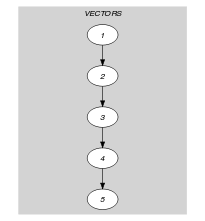
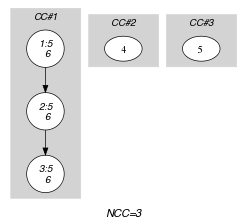
(a)	(b)

Global Constraint Catalog

5. Global Constraint Catalogue

5.306. ordered_atleast_nvector

Figure 5.306.1. Initial and final graph of the 𝚘𝚛𝚍𝚎𝚛𝚎𝚍_𝚊𝚝𝚕𝚎𝚊𝚜𝚝_𝚗𝚟𝚎𝚌𝚝𝚘𝚛 constraint

Figure 5.306.1. Initial and final graph of the $𝚘𝚛𝚍𝚎𝚛𝚎𝚍_𝚊𝚝𝚕𝚎𝚊𝚜𝚝_𝚗𝚟𝚎𝚌𝚝𝚘𝚛$ constraint