Global Constraint Catalog: Cinverse

5.200. inverse_offset

DESCRIPTION

LINKS

GRAPH

Origin

Gecode

Constraint

$𝚒𝚗𝚟𝚎𝚛𝚜𝚎_𝚘𝚏𝚏𝚜𝚎𝚝 (𝚂𝙾𝙵𝙵𝚂𝙴𝚃, 𝙿𝙾𝙵𝙵𝚂𝙴𝚃, 𝙽𝙾𝙳𝙴𝚂)$

Synonym

$𝚌𝚑𝚊𝚗𝚗𝚎𝚕$ .

Arguments

$𝚂𝙾𝙵𝙵𝚂𝙴𝚃$	$𝚒𝚗𝚝$
$𝙿𝙾𝙵𝙵𝚂𝙴𝚃$	$𝚒𝚗𝚝$
$𝙽𝙾𝙳𝙴𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚒𝚗𝚍𝚎𝚡 - 𝚒𝚗𝚝, 𝚜𝚞𝚌𝚌 - 𝚍𝚟𝚊𝚛, 𝚙𝚛𝚎𝚍 - 𝚍𝚟𝚊𝚛)$

Restrictions

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝙽𝙾𝙳𝙴𝚂, [𝚒𝚗𝚍𝚎𝚡, 𝚜𝚞𝚌𝚌, 𝚙𝚛𝚎𝚍])

𝙽𝙾𝙳𝙴𝚂 . 𝚒𝚗𝚍𝚎𝚡 \geq 1

𝙽𝙾𝙳𝙴𝚂 . 𝚒𝚗𝚍𝚎𝚡 \leq | 𝙽𝙾𝙳𝙴𝚂 |

𝚍𝚒𝚜𝚝𝚒𝚗𝚌𝚝

(𝙽𝙾𝙳𝙴𝚂, 𝚒𝚗𝚍𝚎𝚡)

𝙽𝙾𝙳𝙴𝚂 . 𝚜𝚞𝚌𝚌 \geq 1 + 𝚂𝙾𝙵𝙵𝚂𝙴𝚃

𝙽𝙾𝙳𝙴𝚂 . 𝚜𝚞𝚌𝚌 \leq | 𝙽𝙾𝙳𝙴𝚂 | + 𝚂𝙾𝙵𝙵𝚂𝙴𝚃

𝙽𝙾𝙳𝙴𝚂 . 𝚙𝚛𝚎𝚍 \geq 1 + 𝙿𝙾𝙵𝙵𝚂𝙴𝚃

𝙽𝙾𝙳𝙴𝚂 . 𝚙𝚛𝚎𝚍 \leq | 𝙽𝙾𝙳𝙴𝚂 | + 𝙿𝙾𝙵𝙵𝚂𝙴𝚃

Purpose

Enforce each vertex of a digraph to have exactly one predecessor and one successor. In addition the following two statements are equivalent:

The successor of the $i^{t h}$ node minus $𝐒𝐎𝐅𝐅𝐒𝐄𝐓$ is equal to $j$ .
The predecessor of the $j^{t h}$ node minus $𝐏𝐎𝐅𝐅𝐒𝐄𝐓$ is equal to $i$ .

I.e., $𝙽𝙾𝙳𝙴𝚂 [i] . 𝚜𝚞𝚌𝚌 - 𝐒𝐎𝐅𝐅𝐒𝐄𝐓 = j \Leftrightarrow 𝙽𝙾𝙳𝙴𝚂 [j] . 𝚙𝚛𝚎𝚍 - 𝐏𝐎𝐅𝐅𝐒𝐄𝐓 = i$ .

Example

(\begin{matrix} - 1, 0, 〈\begin{matrix} 𝚒𝚗𝚍𝚎𝚡 - 1 & 𝚜𝚞𝚌𝚌 - 4 & 𝚙𝚛𝚎𝚍 - 3, \\ 𝚒𝚗𝚍𝚎𝚡 - 2 & 𝚜𝚞𝚌𝚌 - 2 & 𝚙𝚛𝚎𝚍 - 5, \\ 𝚒𝚗𝚍𝚎𝚡 - 3 & 𝚜𝚞𝚌𝚌 - 0 & 𝚙𝚛𝚎𝚍 - 2, \\ 𝚒𝚗𝚍𝚎𝚡 - 4 & 𝚜𝚞𝚌𝚌 - 6 & 𝚙𝚛𝚎𝚍 - 8, \\ 𝚒𝚗𝚍𝚎𝚡 - 5 & 𝚜𝚞𝚌𝚌 - 1 & 𝚙𝚛𝚎𝚍 - 1, \\ 𝚒𝚗𝚍𝚎𝚡 - 6 & 𝚜𝚞𝚌𝚌 - 7 & 𝚙𝚛𝚎𝚍 - 7, \\ 𝚒𝚗𝚍𝚎𝚡 - 7 & 𝚜𝚞𝚌𝚌 - 5 & 𝚙𝚛𝚎𝚍 - 4, \\ 𝚒𝚗𝚍𝚎𝚡 - 8 & 𝚜𝚞𝚌𝚌 - 3 & 𝚙𝚛𝚎𝚍 - 6 \end{matrix}〉 \end{matrix})

The $𝚒𝚗𝚟𝚎𝚛𝚜𝚎_𝚘𝚏𝚏𝚜𝚎𝚝$ constraint holds since:

$𝙽𝙾𝙳𝙴𝚂 [1] . 𝚜𝚞𝚌𝚌 - (- 1) = 5 \Leftrightarrow 𝙽𝙾𝙳𝙴𝚂 [5] . 𝚙𝚛𝚎𝚍 - 0 = 1$ ,
$𝙽𝙾𝙳𝙴𝚂 [2] . 𝚜𝚞𝚌𝚌 - (- 1) = 3 \Leftrightarrow 𝙽𝙾𝙳𝙴𝚂 [3] . 𝚙𝚛𝚎𝚍 - 0 = 2$ ,
$𝙽𝙾𝙳𝙴𝚂 [3] . 𝚜𝚞𝚌𝚌 - (- 1) = 1 \Leftrightarrow 𝙽𝙾𝙳𝙴𝚂 [1] . 𝚙𝚛𝚎𝚍 - 0 = 3$ ,
$𝙽𝙾𝙳𝙴𝚂 [4] . 𝚜𝚞𝚌𝚌 - (- 1) = 7 \Leftrightarrow 𝙽𝙾𝙳𝙴𝚂 [7] . 𝚙𝚛𝚎𝚍 - 0 = 4$ ,
$𝙽𝙾𝙳𝙴𝚂 [5] . 𝚜𝚞𝚌𝚌 - (- 1) = 2 \Leftrightarrow 𝙽𝙾𝙳𝙴𝚂 [2] . 𝚙𝚛𝚎𝚍 - 0 = 5$ .
$𝙽𝙾𝙳𝙴𝚂 [6] . 𝚜𝚞𝚌𝚌 - (- 1) = 8 \Leftrightarrow 𝙽𝙾𝙳𝙴𝚂 [8] . 𝚙𝚛𝚎𝚍 - 0 = 6$ .
$𝙽𝙾𝙳𝙴𝚂 [7] . 𝚜𝚞𝚌𝚌 - (- 1) = 6 \Leftrightarrow 𝙽𝙾𝙳𝙴𝚂 [6] . 𝚙𝚛𝚎𝚍 - 0 = 7$ .
$𝙽𝙾𝙳𝙴𝚂 [8] . 𝚜𝚞𝚌𝚌 - (- 1) = 4 \Leftrightarrow 𝙽𝙾𝙳𝙴𝚂 [4] . 𝚙𝚛𝚎𝚍 - 0 = 8$ .

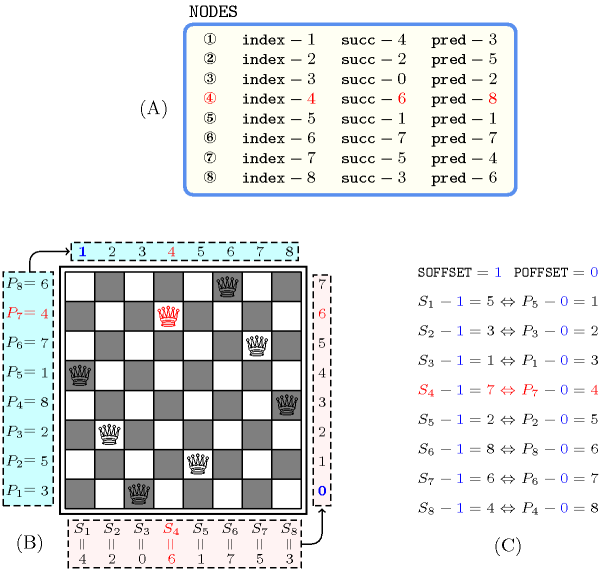
Figure 5.200.1 shows the board that can be associated with this example.

Figure 5.200.1. Example slot where we highlight the fourth item in red showing the relation between $S_{4}$ and $P_{7}$ , where $S_{i}$ and $P_{i}$ (with $1 \leq i \leq 8$ ) respectively stands for the successor and predecessor attributes of the $i^{𝚝𝚑}$ item of the $𝙽𝙾𝙳𝙴𝚂$ collection (A) Collection of nodes passed to the $𝚒𝚗𝚟𝚎𝚛𝚜𝚎_𝚘𝚏𝚏𝚜𝚎𝚝$ constraint, (B) Corresponding board, (C) Conditions linking the successor and the predecessor attributes via the offsets $𝚂𝙾𝙵𝙵𝚂𝙴𝚃 = 1$ and $𝙿𝙾𝙵𝙵𝚂𝙴𝚃 = 0$ .

Typical

𝚂𝙾𝙵𝙵𝚂𝙴𝚃 \geq - 1

𝚂𝙾𝙵𝙵𝚂𝙴𝚃 \leq 1

𝙿𝙾𝙵𝙵𝚂𝙴𝚃 \geq - 1

𝙿𝙾𝙵𝙵𝚂𝙴𝚃 \leq 1

| 𝙽𝙾𝙳𝙴𝚂 | > 1

Symmetry

Items of $𝙽𝙾𝙳𝙴𝚂$ are permutable.

Arg. properties

Functional dependency: $𝙽𝙾𝙳𝙴𝚂 . 𝚜𝚞𝚌𝚌$ determined by $𝚂𝙾𝙵𝙵𝚂𝙴𝚃$ , $𝙿𝙾𝙵𝙵𝚂𝙴𝚃$ , $𝙽𝙾𝙳𝙴𝚂 . 𝚒𝚗𝚍𝚎𝚡$ and $𝙽𝙾𝙳𝙴𝚂 . 𝚙𝚛𝚎𝚍$ .
Functional dependency: $𝙽𝙾𝙳𝙴𝚂 . 𝚙𝚛𝚎𝚍$ determined by $𝚂𝙾𝙵𝙵𝚂𝙴𝚃$ , $𝙿𝙾𝙵𝙵𝚂𝙴𝚃$ , $𝙽𝙾𝙳𝙴𝚂 . 𝚒𝚗𝚍𝚎𝚡$ and $𝙽𝙾𝙳𝙴𝚂 . 𝚜𝚞𝚌𝚌$ .

Remark

The $𝚒𝚗𝚟𝚎𝚛𝚜𝚎_𝚘𝚏𝚏𝚜𝚎𝚝$ constraint is called $𝚌𝚑𝚊𝚗𝚗𝚎𝚕$ in Gecode (http://www.gecode.org/). Having two offsets was motivated by the fact that it is possible to declare arrays at any position in the MiniZinc modelling language.

Systems

inverseChanneling in Choco, channel in Gecode.

See also

specialisation: $𝚒𝚗𝚟𝚎𝚛𝚜𝚎$ (assume that $𝚂𝙾𝙵𝙵𝚂𝙴𝚃$ and $𝙿𝙾𝙵𝙵𝚂𝙴𝚃$ are both equal to 0).

Keywords

constraint arguments: pure functional dependency.

constraint type: graph constraint.

filtering: arc-consistency.

heuristics: heuristics.

modelling: channelling constraint, dual model, functional dependency.

Arc input(s)

$𝙽𝙾𝙳𝙴𝚂$

Arc generator

𝐶𝐿𝐼𝑄𝑈𝐸

\mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚗𝚘𝚍𝚎𝚜 1, 𝚗𝚘𝚍𝚎𝚜 2)

Arc arity

Arc constraint(s)

• 𝚗𝚘𝚍𝚎𝚜 1 . 𝚜𝚞𝚌𝚌 - 𝚂𝙾𝙵𝙵𝚂𝙴𝚃 = 𝚗𝚘𝚍𝚎𝚜 2 . 𝚒𝚗𝚍𝚎𝚡

• 𝚗𝚘𝚍𝚎𝚜 2 . 𝚙𝚛𝚎𝚍 - 𝙿𝙾𝙵𝙵𝚂𝙴𝚃 = 𝚗𝚘𝚍𝚎𝚜 1 . 𝚒𝚗𝚍𝚎𝚡

Graph property(ies)

𝐍𝐀𝐑𝐂

= | 𝙽𝙾𝙳𝙴𝚂 |

Graph model

In order to express the binary constraint that links two vertices one has to make explicit the identifier of the vertices. This is why the $𝚒𝚗𝚟𝚎𝚛𝚜𝚎_𝚘𝚏𝚏𝚜𝚎𝚝$ constraint considers objects that have three attributes:

One fixed attribute $𝚒𝚗𝚍𝚎𝚡$ that is the identifier of the vertex,
One variable attribute $𝚜𝚞𝚌𝚌$ that is the successor of the vertex,
One variable attribute $𝚙𝚛𝚎𝚍$ that is the predecessor of the vertex.

Parts (A) and (B) of Figure 5.200.2 respectively show the initial and final graph associated with the Example slot. Since we use the $𝐍𝐀𝐑𝐂$ graph property, the arcs of the final graph are stressed in bold.

Figure 5.200.2. Initial and final graph of the $𝚒𝚗𝚟𝚎𝚛𝚜𝚎_𝚘𝚏𝚏𝚜𝚎𝚝$ constraint


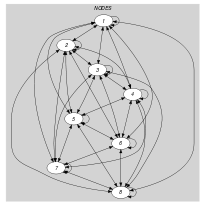
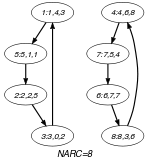
(a)	(b)

Global Constraint Catalog

5. Global Constraint Catalogue

5.200. inverse_offset

Figure 5.200.2. Initial and final graph of the 𝚒𝚗𝚟𝚎𝚛𝚜𝚎_𝚘𝚏𝚏𝚜𝚎𝚝 constraint

Figure 5.200.2. Initial and final graph of the $𝚒𝚗𝚟𝚎𝚛𝚜𝚎_𝚘𝚏𝚏𝚜𝚎𝚝$ constraint