Global Constraint Catalog: Cbalance

5.43. balance

DESCRIPTION

LINKS

GRAPH

AUTOMATON

Origin

N. Beldiceanu

Constraint

$𝚋𝚊𝚕𝚊𝚗𝚌𝚎 (𝙱𝙰𝙻𝙰𝙽𝙲𝙴, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

Arguments

$𝙱𝙰𝙻𝙰𝙽𝙲𝙴$	$𝚍𝚟𝚊𝚛$
$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)$

Restrictions

𝙱𝙰𝙻𝙰𝙽𝙲𝙴 \geq 0

𝙱𝙰𝙻𝙰𝙽𝙲𝙴 \leq 𝚖𝚊𝚡 (0, | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | - 2)

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚟𝚊𝚛)

Purpose

$𝙱𝙰𝙻𝙰𝙽𝙲𝙴$ is equal to the difference between the number of occurrence of the value that occurs the most and the value that occurs the least within the collection of variables $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ .

Example

(2, 〈3, 1, 7, 1, 1〉)

(0, 〈3, 3, 1, 1, 1, 3〉)

(4, 〈3, 1, 1, 1, 1, 1〉)

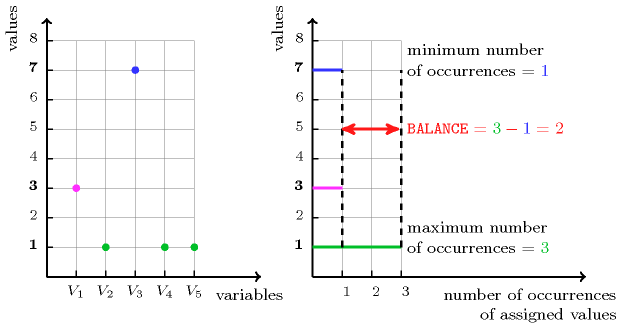
In the first example, values $1, 3$ and 7 are respectively used $3, 1$ and 1 times. The corresponding $𝚋𝚊𝚕𝚊𝚗𝚌𝚎$ constraint holds since its first argument $𝙱𝙰𝙻𝙰𝙽𝙲𝙴$ is assigned to the difference between the maximum and minimum number of the previous occurrences (i.e., $3 - 1$ ). Figure 5.43.1 shows the solution associated with this first example.

Figure 5.43.1. Illustration of the first example of the Example slot: five variables $V_{1}$ , $V_{2}$ , $V_{3}$ , $V_{4}$ , $V_{5}$ respectively fixed to values 3, 1, 7, 1 and 1, and the corresponding value of $𝙱𝙰𝙻𝙰𝙽𝙲𝙴 = 2$

All solutions

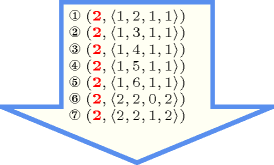
Figure 5.43.2 gives all solutions to the following non ground instance of the $𝚋𝚊𝚕𝚊𝚗𝚌𝚎$ constraint: $𝙱𝙰𝙻𝙰𝙽𝙲𝙴 \in [2, 3]$ , $V_{1} \in [0, 5]$ , $V_{2} \in [2, 6]$ , $V_{3} \in [0, 1]$ , $V_{4} \in [1, 2]$ , $𝚋𝚊𝚕𝚊𝚗𝚌𝚎$ $(𝙱𝙰𝙻𝙰𝙽𝙲𝙴, 〈 V_{1}, V_{2}, V_{3}, V_{4} 〉)$ .

Figure 5.43.2. All solutions corresponding to the non ground example of the $𝚋𝚊𝚕𝚊𝚗𝚌𝚎$ constraint of the All solutions slot

Typical

𝙱𝙰𝙻𝙰𝙽𝙲𝙴 \leq 2 + | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | / 10

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | > 2

Symmetries

Items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ are permutable.
All occurrences of two distinct values of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛$ can be swapped; all occurrences of a value of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛$ can be renamed to any unused value.

Arg. properties

Functional dependency: $𝙱𝙰𝙻𝙰𝙽𝙲𝙴$ determined by $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ .

Usage

An application of the $𝚋𝚊𝚕𝚊𝚗𝚌𝚎$ constraint is to enforce a balanced assignment of values, no matter how many distinct values will be used. In this case one will push down the maximum value of the first argument of the $𝚋𝚊𝚕𝚊𝚗𝚌𝚎$ constraint.

Remark

If we do not want to use an automaton with an array of counters a possible reformulation of the $𝚋𝚊𝚕𝚊𝚗𝚌𝚎$ constraint can be achieved in the following way. We use a $𝚜𝚘𝚛𝚝$ constraint in order to reorder the variables of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ and compute the difference between the longest and the smallest sequences of consecutive values.

Counting

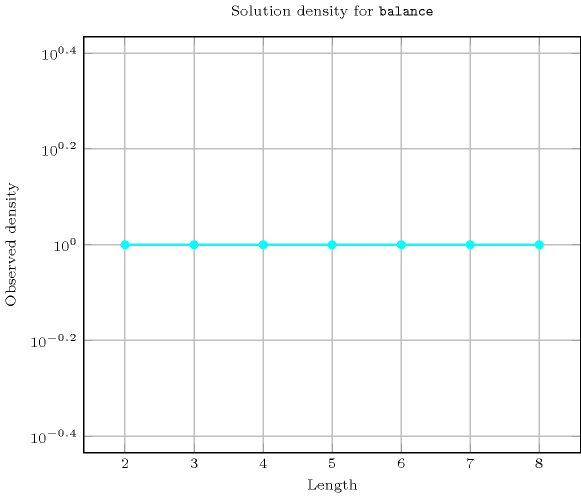
Length ( $n$ )	2	3	4	5	6	7	8
Solutions	9	64	625	7776	117649	2097152	43046721

Number of solutions for $𝚋𝚊𝚕𝚊𝚗𝚌𝚎$ : domains $0 . . n$

ctrs/balance-3-tikz

ctrs/balance-4-tikz

Length (

n

)

Total

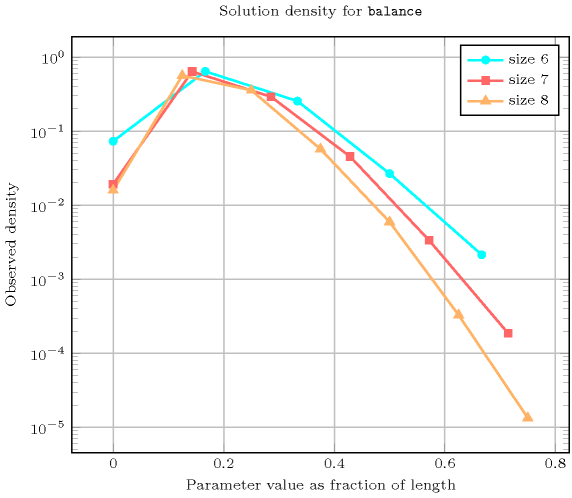
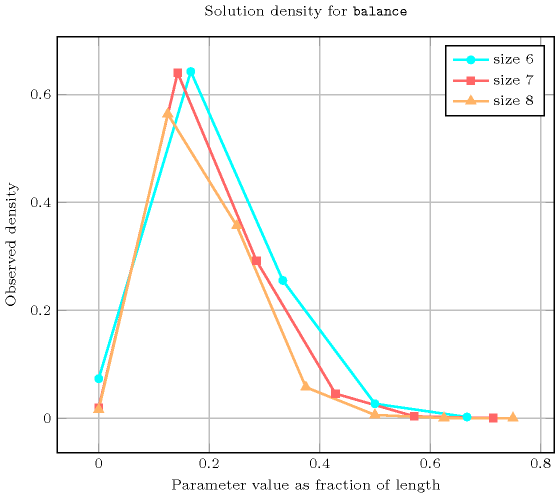
625

7776

117649

2097152

43046721

Parameter

value

185

726

8617

40328

682929

360

5700

75600

1342600

24272640

1200

30030

611520

15350832

150

3150

95256

2469600

252

7056

256032

392

14112

576

Solution count for $𝚋𝚊𝚕𝚊𝚗𝚌𝚎$ : domains $0 . . n$

ctrs/balance-5-tikz

ctrs/balance-6-tikz

See also

generalisation: $𝚋𝚊𝚕𝚊𝚗𝚌𝚎_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕$ ( $𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎$ replaced by $𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎 / 𝚌𝚘𝚗𝚜𝚝𝚊𝚗𝚝$ ), $𝚋𝚊𝚕𝚊𝚗𝚌𝚎_𝚖𝚘𝚍𝚞𝚕𝚘$ ( $𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎$ replaced by $𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎 \mod 𝚌𝚘𝚗𝚜𝚝𝚊𝚗𝚝$ ), $𝚋𝚊𝚕𝚊𝚗𝚌𝚎_𝚙𝚊𝚛𝚝𝚒𝚝𝚒𝚘𝚗$ ( $𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎$ replaced by $𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎 \in 𝚙𝚊𝚛𝚝𝚒𝚝𝚒𝚘𝚗$ ).

implies: $𝚜𝚘𝚏𝚝_𝚊𝚕𝚕_𝚎𝚚𝚞𝚊𝚕_𝚖𝚒𝚗_𝚌𝚝𝚛$ .

related: $𝚋𝚊𝚕𝚊𝚗𝚌𝚎_𝚌𝚢𝚌𝚕𝚎$ (balanced assignment versus graph partitionning with balanced cycles), $𝚋𝚊𝚕𝚊𝚗𝚌𝚎_𝚙𝚊𝚝𝚑$ (balanced assignment versus graph partitionning with balanced paths), $𝚋𝚊𝚕𝚊𝚗𝚌𝚎_𝚝𝚛𝚎𝚎$ (balanced assignment versus graph partitionning with balanced trees), $𝚗𝚟𝚊𝚕𝚞𝚎$ (no restriction on how balanced an assignment is), $𝚝𝚛𝚎𝚎_𝚛𝚊𝚗𝚐𝚎$ (balanced assignment versus balanced tree).

shift of concept: $𝚎𝚚𝚞𝚒𝚕𝚒𝚋𝚛𝚒𝚞𝚖$ .

Keywords

application area: assignment.

characteristic of a constraint: automaton, automaton with array of counters.

constraint arguments: pure functional dependency.

constraint type: value constraint.

final graph structure: equivalence.

modelling: balanced assignment, functional dependency.

Arc input(s)

$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$

Arc generator

𝐶𝐿𝐼𝑄𝑈𝐸

\mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1, 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2)

Arc arity

Arc constraint(s)

𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1 . 𝚟𝚊𝚛 = 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2 . 𝚟𝚊𝚛

Graph property(ies)

𝐑𝐀𝐍𝐆𝐄_𝐍𝐒𝐂𝐂

= 𝙱𝙰𝙻𝙰𝙽𝙲𝙴

Graph class

𝙴𝚀𝚄𝙸𝚅𝙰𝙻𝙴𝙽𝙲𝙴

Graph model

The graph property $𝐑𝐀𝐍𝐆𝐄_𝐍𝐒𝐂𝐂$ constraints the difference between the sizes of the largest and smallest strongly connected components.

Parts (A) and (B) of Figure 5.43.3 respectively show the initial and final graph associated with the first example of the Example slot. Since we use the $𝐑𝐀𝐍𝐆𝐄_𝐍𝐒𝐂𝐂$ graph property, we show the largest and smallest strongly connected components of the final graph.

Figure 5.43.3. Initial and final graph of the $𝚋𝚊𝚕𝚊𝚗𝚌𝚎$ constraint


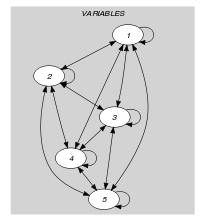
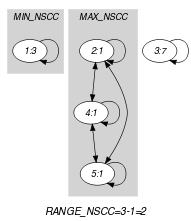
(a)	(b)

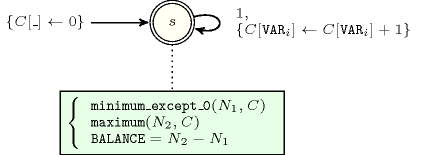
Automaton: Figure 5.43.4 depicts the automaton associated with the $𝚋𝚊𝚕𝚊𝚗𝚌𝚎$ constraint. To each item of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ corresponds a signature variable $S_{i}$ that is equal to 1.

Figure 5.43.4. Automaton of the $𝚋𝚊𝚕𝚊𝚗𝚌𝚎$ constraint

Global Constraint Catalog

5. Global Constraint Catalogue

5.43. balance

Figure 5.43.1. Illustration of the first example of the Example slot: five variables $V_{1}$ , $V_{2}$ , $V_{3}$ , $V_{4}$ , $V_{5}$ respectively fixed to values 3, 1, 7, 1 and 1, and the corresponding value of $𝙱𝙰𝙻𝙰𝙽𝙲𝙴 = 2$

Figure 5.43.2. All solutions corresponding to the non ground example of the $𝚋𝚊𝚕𝚊𝚗𝚌𝚎$ constraint of the All solutions slot

Figure 5.43.3. Initial and final graph of the $𝚋𝚊𝚕𝚊𝚗𝚌𝚎$ constraint

Figure 5.43.4. Automaton of the $𝚋𝚊𝚕𝚊𝚗𝚌𝚎$ constraint

Global Constraint Catalog

5. Global Constraint Catalogue

5.43. balance

Figure 5.43.1. Illustration of the first example of the Example slot: five variables V 1 , V 2 , V 3 , V 4 , V 5 respectively fixed to values 3, 1, 7, 1 and 1, and the corresponding value of 𝙱𝙰𝙻𝙰𝙽𝙲𝙴=2

Figure 5.43.2. All solutions corresponding to the non ground example of the 𝚋𝚊𝚕𝚊𝚗𝚌𝚎 constraint of the All solutions slot

Figure 5.43.3. Initial and final graph of the 𝚋𝚊𝚕𝚊𝚗𝚌𝚎 constraint

Figure 5.43.4. Automaton of the 𝚋𝚊𝚕𝚊𝚗𝚌𝚎 constraint

Figure 5.43.1. Illustration of the first example of the Example slot: five variables $V_{1}$ , $V_{2}$ , $V_{3}$ , $V_{4}$ , $V_{5}$ respectively fixed to values 3, 1, 7, 1 and 1, and the corresponding value of $𝙱𝙰𝙻𝙰𝙽𝙲𝙴 = 2$

Figure 5.43.2. All solutions corresponding to the non ground example of the $𝚋𝚊𝚕𝚊𝚗𝚌𝚎$ constraint of the All solutions slot

Figure 5.43.3. Initial and final graph of the $𝚋𝚊𝚕𝚊𝚗𝚌𝚎$ constraint

Figure 5.43.4. Automaton of the $𝚋𝚊𝚕𝚊𝚗𝚌𝚎$ constraint