Global Constraint Catalog: Cmin_dist_between

5.253. min_dist_between_inflexion

DESCRIPTION

LINKS

AUTOMATON

Origin

Derived from $𝚒𝚗𝚏𝚕𝚎𝚡𝚒𝚘𝚗$

Constraint

$𝚖𝚒𝚗_𝚍𝚒𝚜𝚝_𝚋𝚎𝚝𝚠𝚎𝚎𝚗_𝚒𝚗𝚏𝚕𝚎𝚡𝚒𝚘𝚗 (𝙼𝙸𝙽𝙳𝙸𝚂𝚃, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

Arguments

$𝙼𝙸𝙽𝙳𝙸𝚂𝚃$	$𝚒𝚗𝚝$
$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)$

Restrictions

𝙼𝙸𝙽𝙳𝙸𝚂𝚃 \geq 0

𝙼𝙸𝙽𝙳𝙸𝚂𝚃 \leq | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚟𝚊𝚛)

Purpose

Given an integer value $𝙼𝙸𝙽𝙳𝙸𝚂𝚃$ and a sequence of variables $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ enforce $𝙼𝙸𝙽𝙳𝙸𝚂𝚃$ to be greater than or equal to the smallest distance between two consecutive inflexions in the sequence $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ , or to $| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |$ if no more than one inflexion exists.

An inflexion of a sequence of variables $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ is a set of consecutive variables $V_{i}, V_{i + 1}, \dots, V_{j - 1}, V_{j}$ ( $i + 1 < j$ ) such that one of the following conditions holds:

$V_{i} < V_{i + 1} \land V_{i + 1} = \dots = V_{j - 1} \land V_{j - 1} > V_{j}$ ,
$V_{i} > V_{i + 1} \land V_{i + 1} = \dots = V_{j - 1} \land V_{j - 1} < V_{j}$ .

In this context, the index $j$ is the position of the inflexion (i.e., the first instant when the inflexion is discovered when scanning the sequence of variables $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ from left to right. The distance between two consecutive inflexions is the absolute value of the difference of their corresponding positions.

Example

(2, 〈2, 2, 3, 3, 2, 2, 1, 4, 4, 3〉)

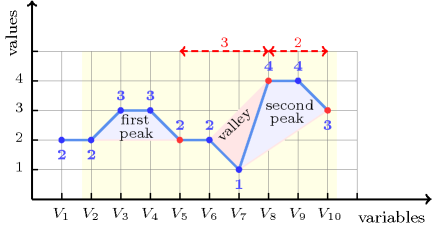
Figure 5.253.1 shows the three inflexions associated with the sequence 2, 2, 3, 3, 2, 2, 1, 4, 4, 3 and their respective positions 5, 8 and 10 in red. The $𝚖𝚒𝚗_𝚍𝚒𝚜𝚝_𝚋𝚎𝚝𝚠𝚎𝚎𝚗_𝚒𝚗𝚏𝚕𝚎𝚡𝚒𝚘𝚗$ constraint holds since its first argument $𝙼𝙸𝙽𝙳𝙸𝚂𝚃 = 2$ is greater than or equal to the smallest distance 2 between two consecutive inflexions of the sequence of variables $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ .

Figure 5.253.1. Illustration of the Example slot: a sequence of ten variables $V_{1}$ , $V_{2}$ , $V_{3}$ , $V_{4}$ , $V_{5}$ , $V_{6}$ , $V_{7}$ , $V_{8}$ , $V_{9}$ , $V_{10}$ respectively fixed to values 2, 2, 3, 3, 2, 2, 1, 4, 4, 3 and its three inflexions, two peaks and one valley; each red point denotes an instant where a new inflexion is discovered while scanning the sequence from left to right; as shown by the rightmost arrow, the minimum distance between two consecutive inflexions is equal to 2.

Typical

𝙼𝙸𝙽𝙳𝙸𝚂𝚃 > 1

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | > 3

𝚛𝚊𝚗𝚐𝚎

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) > 1

Symmetries

Items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ can be reversed.
One and the same constant can be added to the $𝚟𝚊𝚛$ attribute of all items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ .

Counting

Length ( $n$ )	2	3	4	5	6	7	8
Solutions	9	64	1135	25444	574483	13287476	328156407

Number of solutions for $𝚖𝚒𝚗_𝚍𝚒𝚜𝚝_𝚋𝚎𝚝𝚠𝚎𝚎𝚗_𝚒𝚗𝚏𝚕𝚎𝚡𝚒𝚘𝚗$ : domains $0 . . n$

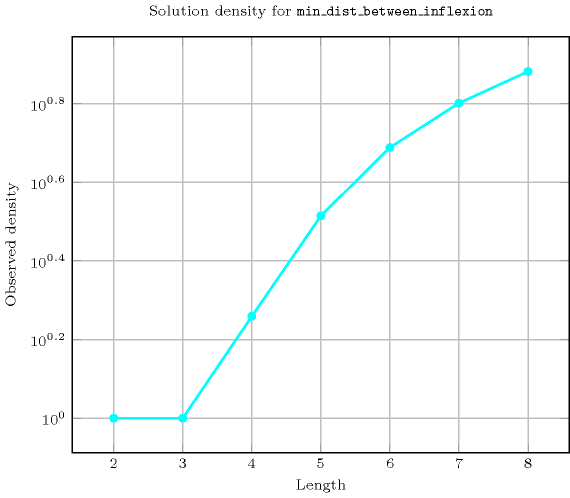
ctrs/min_dist_between_inflexion-2-tikz

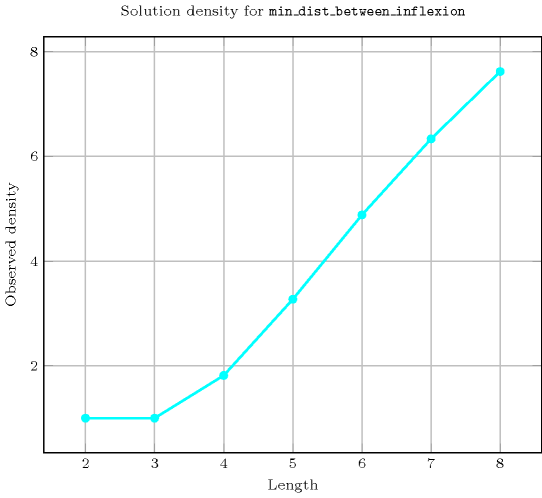
ctrs/min_dist_between_inflexion-3-tikz

Length (

n

)

Total

1135

25444

574483

13287476

328156407

Parameter

value

170

3598

73794

1543512

35152278

170

4690

91098

1819764

39992562

170

4690

97314

1932012

41360676

625

4690

97314

1965012

42025560

7776

97314

1965012

42192870

117649

1965012

42192870

2097152

42192870

43046721

Solution count for $𝚖𝚒𝚗_𝚍𝚒𝚜𝚝_𝚋𝚎𝚝𝚠𝚎𝚎𝚗_𝚒𝚗𝚏𝚕𝚎𝚡𝚒𝚘𝚗$ : domains $0 . . n$

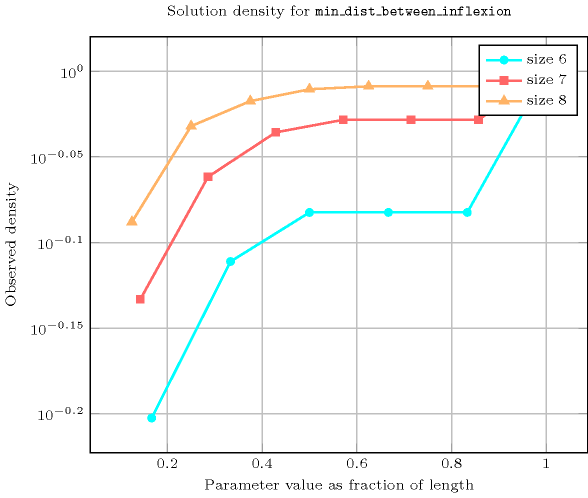
ctrs/min_dist_between_inflexion-4-tikz

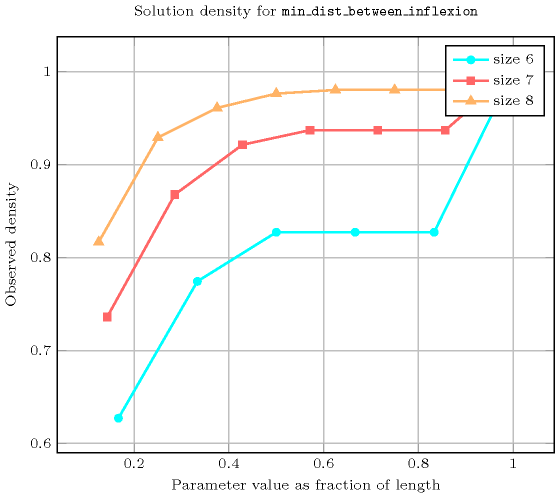
ctrs/min_dist_between_inflexion-5-tikz

Keywords

characteristic of a constraint: automaton, automaton with counters, automaton with same input symbol.

combinatorial object: sequence.

constraint network structure: sliding cyclic(1) constraint network(3).

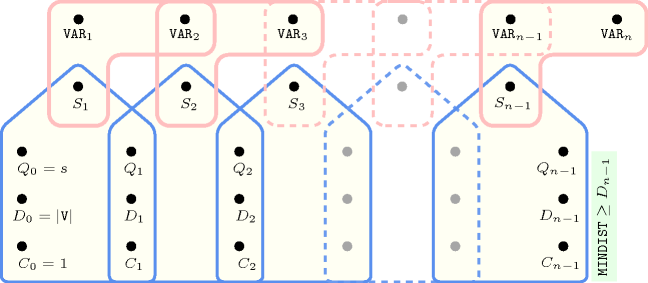
Automaton: Figure 5.253.2 depicts the automaton associated with the $𝚖𝚒𝚗_𝚍𝚒𝚜𝚝_𝚋𝚎𝚝𝚠𝚎𝚎𝚗_𝚒𝚗𝚏𝚕𝚎𝚡𝚒𝚘𝚗$ constraint.

Figure 5.253.2. Automaton of the $𝚖𝚒𝚗_𝚍𝚒𝚜𝚝_𝚋𝚎𝚝𝚠𝚎𝚎𝚗_𝚒𝚗𝚏𝚕𝚎𝚡𝚒𝚘𝚗$ constraint (state $s$ means that we are in stationary mode, state $i 0$ means that we are in increasing mode and that we did not yet found any inflexion, state $d 0$ means that we are in decreasing mode and that we did not yet found any inflexion, state $i 1$ means that we are in increasing mode and that we already found at least one inflexion, state $d 1$ means that we are in decreasing mode and that we already found at least one inflexion, the minimum distance between two consecutive inflexions is updated each time we switch from $i 1$ to $d 1$ mode – or conversely from $d 1$ to $i 1$ mode – and the counter $D$ is updated accordingly)

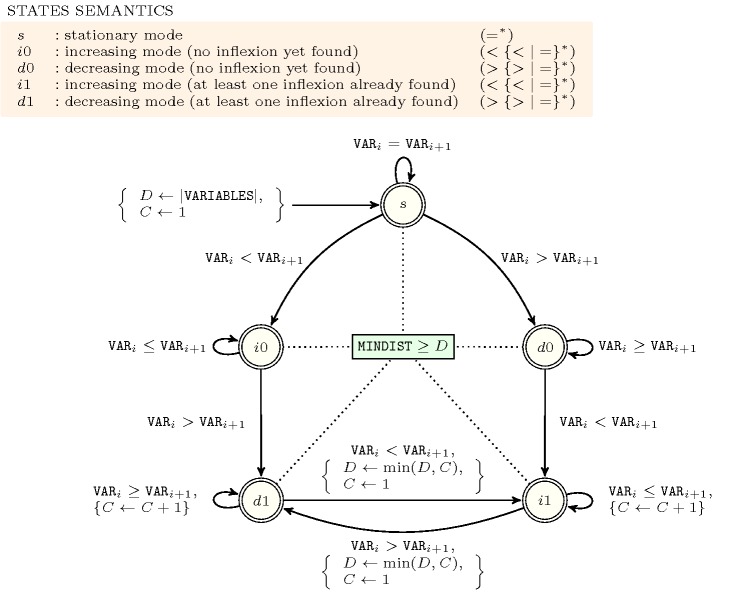
Figure 5.253.3. Hypergraph of the reformulation corresponding to the automaton of the $𝚖𝚒𝚗_𝚍𝚒𝚜𝚝_𝚋𝚎𝚝𝚠𝚎𝚎𝚗_𝚒𝚗𝚏𝚕𝚎𝚡𝚒𝚘𝚗$ constraint where $𝚅$ is a shortcut for $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ (since all states of the automaton are accepting there is no restriction on the last variable $Q_{n - 1}$ )

Global Constraint Catalog

5. Global Constraint Catalogue

5.253. min_dist_between_inflexion