5.44. balance_cycle
| DESCRIPTION | LINKS | GRAPH |
- Origin
- Constraint
- Arguments
- Restrictions
- Purpose
Consider a digraph described by the collection. Partition into a set of vertex disjoint circuits in such a way that each vertex of belongs to a single circuit. is equal to the difference between the number of vertices of the largest circuit and the number of vertices of the smallest circuit.
- Example
-
In the first example we have the following two circuits: and . Since is the difference between the number of vertices of the largest circuit (i.e., 3) and the number of vertices of the smallest circuit (i.e., 2) the corresponding constraint holds.
- All solutions
Figure 5.44.1 gives all solutions to the following non ground instance of the constraint: , , , , , , .
Figure 5.44.1. All solutions corresponding to the non ground example of the constraint of the All solutions slot; the attribute is displayed as indices of the attribute, and all vertices of a same cycle are coloured by the same colour.

- Typical
- Symmetry
Items of are permutable.
- Arg. properties
Functional dependency: determined by .
- Counting
-
Length () 2 3 4 5 6 7 8 9 10 Solutions 2 6 24 120 720 5040 40320 362880 3628800 Number of solutions for : domains
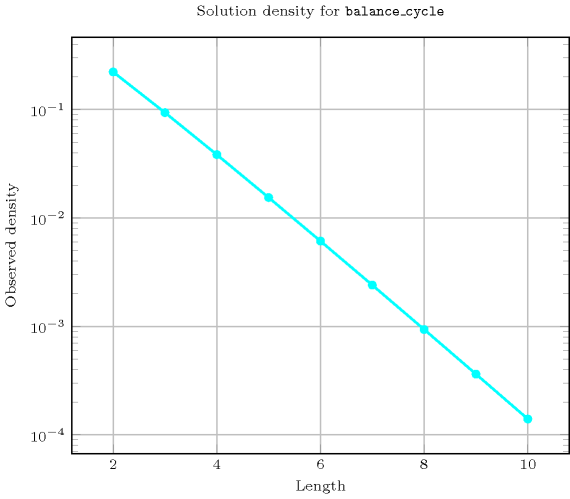
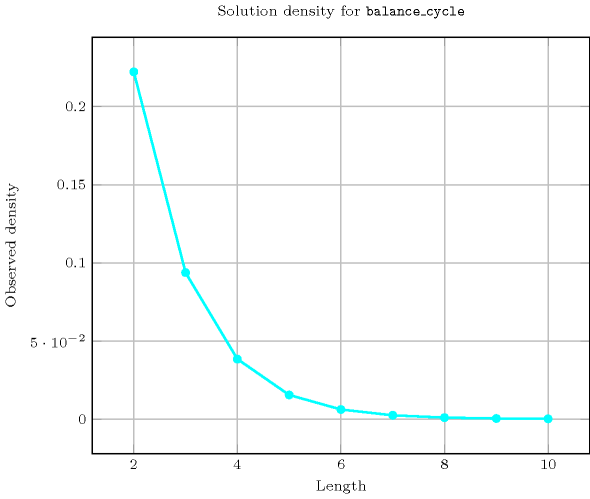
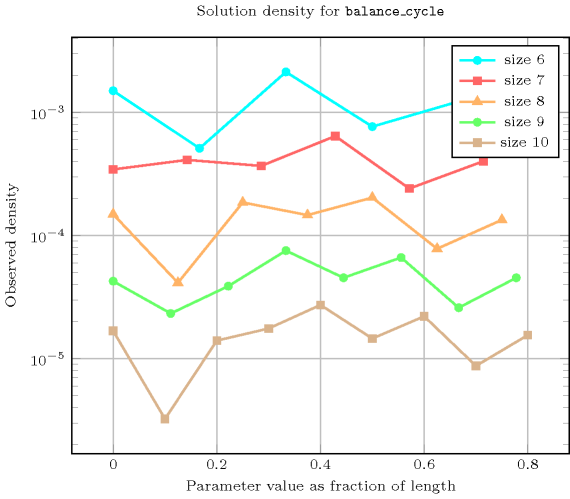
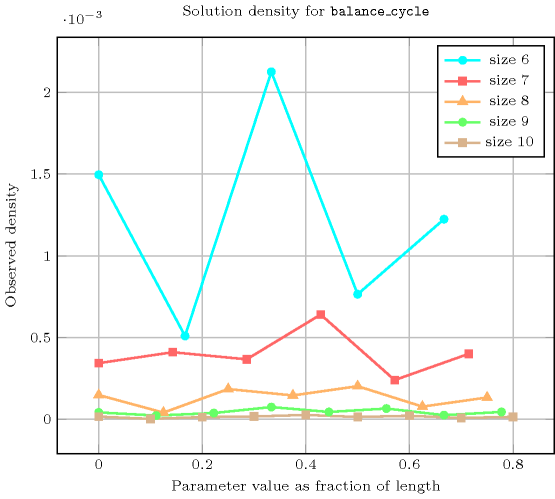
Length () 2 3 4 5 6 7 8 9 10 Total 2 6 24 120 720 5040 40320 362880 3628800 Parameter value 0 2 3 10 25 176 721 6406 42561 436402 1 - 3 6 45 60 861 1778 23283 84150 2 - - 8 20 250 770 7980 38808 363680 3 - - - 30 90 1344 6300 75348 456120 4 - - - - 144 504 8736 45360 708048 5 - - - - - 840 3360 66240 378000 6 - - - - - - 5760 25920 572400 7 - - - - - - - 45360 226800 8 - - - - - - - - 403200 Solution count for : domains
- See also
related: (equivalence classes correspond to vertices in same cycle rather than variables assigned to the same value), (do not care how many cycles but how balanced the cycles are).
- Keywords
combinatorial object: permutation.
constraint type: graph constraint, graph partitioning constraint.
final graph structure: circuit, connected component, strongly connected component, one_succ.
- Cond. implications
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
- Graph property(ies)
-
- Graph class
-
- Graph model
From the restrictions and from the arc constraint, we deduce that we have a bijection from the successor variables to the values of interval . With no explicit restrictions it would have been impossible to derive this property.
In order to express the binary constraint that links two vertices one has to make explicit the identifier of the vertices. This is why the constraint considers objects that have two attributes:
One fixed attribute that is the identifier of the vertex,
One variable attribute that is the successor of the vertex.
The graph property 0 is used in order to avoid having vertices that both do not belong to a circuit and have at least one successor located on a circuit. This concretely means that all vertices of the final graph should belong to a circuit.
Parts (A) and (B) of Figure 5.44.2 respectively show the initial and final graph associated with the first example of the Example slot. Since we use the graph property, we show the connected components of the final graph. The constraint holds since all the vertices belong to a circuit (i.e., 0) and since 1.
Figure 5.44.2. Initial and final graph of the constraint
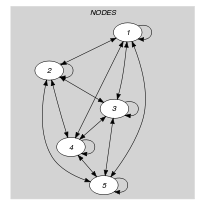
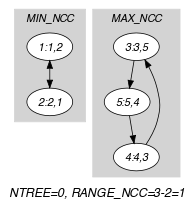
(a) (b)