5.177. in
| DESCRIPTION | LINKS | GRAPH | AUTOMATON |
- Origin
Domain definition.
- Constraint
- Synonyms
, , .
- Arguments
- Restrictions
- Purpose
Enforce the domain variable to take a value within the values described by the collection.
- Example
-
The constraint holds since its first argument occurs within the collection of values .
- Typical
- Symmetries
Items of are permutable.
can be set to any value of .
One and the same constant can be added to as well as to the attribute of all items of .
- Arg. properties
Extensible wrt. .
- Remark
Entailment occurs immediately after posting this constraint.
The constraint is called in Gecode (http://www.gecode.org/), and in MiniZinc (http://www.minizinc.org/). In MiniZinc the attribute is not necessarily fixed, i.e. it can be a domain variable.
- Systems
member in Choco, rel in Gecode, dom in Gecode, in in JaCoP, member in MiniZinc, in in SICStus, in_set in SICStus.
- Used in
- See also
common keyword: (domain definition), , , (value constraint).
implied by: , .
implies: .
- Keywords
characteristic of a constraint: automaton, automaton without counters, reified automaton constraint, derived collection.
constraint arguments: unary constraint.
constraint network structure: centered cyclic(1) constraint network(1).
- Derived Collection
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
- Graph property(ies)
-
- Graph model
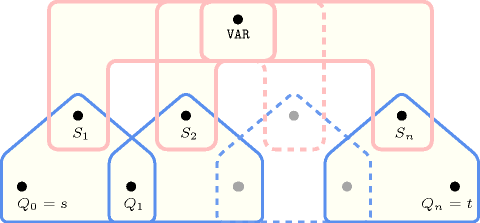
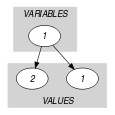
Parts (A) and (B) of Figure 5.177.1 respectively show the initial and final graph associated with the Example slot. Since we use the graph property, the unique arc of the final graph is stressed in bold.
Figure 5.177.1. Initial and final graph of the constraint
(a) (b) - Signature
Since all the attributes of the collection are distinct and because of the arc constraint the final graph contains at most one arc. Therefore we can rewrite to and simplify to .
- Automaton
Figure 5.177.2 depicts the automaton associated with the constraint. Let be the attribute of the item of the collection. To each pair corresponds a 0-1 signature variable as well as the following signature constraint: .
Figure 5.177.2. Automaton of the constraint
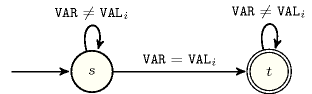
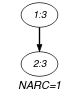
Figure 5.177.3. Hypergraph of the reformulation corresponding to the automaton of the constraint