Global Constraint Catalog: Cinverse

5.201. inverse_set

DESCRIPTION

LINKS

GRAPH

Origin

Derived from $𝚒𝚗𝚟𝚎𝚛𝚜𝚎$ .

Constraint

$𝚒𝚗𝚟𝚎𝚛𝚜𝚎_𝚜𝚎𝚝 (𝚇, 𝚈)$

Arguments

$𝚇$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚒𝚗𝚍𝚎𝚡 - 𝚒𝚗𝚝, 𝚜𝚎𝚝 - 𝚜𝚟𝚊𝚛)$
$𝚈$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚒𝚗𝚍𝚎𝚡 - 𝚒𝚗𝚝, 𝚜𝚎𝚝 - 𝚜𝚟𝚊𝚛)$

Restrictions

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚇, [𝚒𝚗𝚍𝚎𝚡, 𝚜𝚎𝚝])

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚈, [𝚒𝚗𝚍𝚎𝚡, 𝚜𝚎𝚝])

𝚒𝚗𝚌𝚛𝚎𝚊𝚜𝚒𝚗𝚐_𝚜𝚎𝚚

(𝚇, 𝚒𝚗𝚍𝚎𝚡)

𝚒𝚗𝚌𝚛𝚎𝚊𝚜𝚒𝚗𝚐_𝚜𝚎𝚚

(𝚈, 𝚒𝚗𝚍𝚎𝚡)

𝚇 . 𝚒𝚗𝚍𝚎𝚡 \geq 1

𝚇 . 𝚒𝚗𝚍𝚎𝚡 \leq | 𝚇 |

𝚈 . 𝚒𝚗𝚍𝚎𝚡 \geq 1

𝚈 . 𝚒𝚗𝚍𝚎𝚡 \leq | 𝚈 |

𝚇 . 𝚜𝚎𝚝 \geq 1

𝚇 . 𝚜𝚎𝚝 \leq | 𝚈 |

𝚈 . 𝚜𝚎𝚝 \geq 1

𝚈 . 𝚜𝚎𝚝 \leq | 𝚇 |

Purpose

The following two statements are equivalent:

Value $j$ belongs to the set variable of the $i^{t h}$ item of the $𝚇$ collection.
Value $i$ belongs to the set variable of the $j^{t h}$ item of the $𝚈$ collection.

I.e., $j \in 𝚇 [i] \Leftrightarrow i \in 𝚈 [j]$ .

Example

(\begin{matrix} 〈\begin{matrix} 𝚒𝚗𝚍𝚎𝚡 - 1 & 𝚜𝚎𝚝 - {2, 4}, \\ 𝚒𝚗𝚍𝚎𝚡 - 2 & 𝚜𝚎𝚝 - {4}, \\ 𝚒𝚗𝚍𝚎𝚡 - 3 & 𝚜𝚎𝚝 - {1}, \\ 𝚒𝚗𝚍𝚎𝚡 - 4 & 𝚜𝚎𝚝 - {4} \end{matrix}〉, \\ 〈\begin{matrix} 𝚒𝚗𝚍𝚎𝚡 - 1 & 𝚜𝚎𝚝 - {3}, \\ 𝚒𝚗𝚍𝚎𝚡 - 2 & 𝚜𝚎𝚝 - {1}, \\ 𝚒𝚗𝚍𝚎𝚡 - 3 & 𝚜𝚎𝚝 - \emptyset, \\ 𝚒𝚗𝚍𝚎𝚡 - 4 & 𝚜𝚎𝚝 - {1, 2, 4}, \\ 𝚒𝚗𝚍𝚎𝚡 - 5 & 𝚜𝚎𝚝 - \emptyset \end{matrix}〉 \end{matrix})

The $𝚒𝚗𝚟𝚎𝚛𝚜𝚎_𝚜𝚎𝚝$ constraint holds since:

$\{\begin{matrix} 2 \in 𝚇 [1] . 𝚜𝚎𝚝 \Leftrightarrow 1 \in 𝚈 [2] . 𝚜𝚎𝚝, & 4 \in 𝚇 [1] . 𝚜𝚎𝚝 \Leftrightarrow 1 \in 𝚈 [4] . 𝚜𝚎𝚝, \\ 4 \in 𝚇 [2] . 𝚜𝚎𝚝 \Leftrightarrow 2 \in 𝚈 [4] . 𝚜𝚎𝚝, \\ 1 \in 𝚇 [3] . 𝚜𝚎𝚝 \Leftrightarrow 3 \in 𝚈 [1] . 𝚜𝚎𝚝, \\ 4 \in 𝚇 [4] . 𝚜𝚎𝚝 \Leftrightarrow 4 \in 𝚈 [4] . 𝚜𝚎𝚝 . \end{matrix}$

Typical

| 𝚇 | > 1

| 𝚈 | > 1

Symmetries

Arguments are permutable w.r.t. permutation $(𝚇, 𝚈)$ .
Items of $𝚇$ are permutable.
Items of $𝚈$ are permutable.

Usage

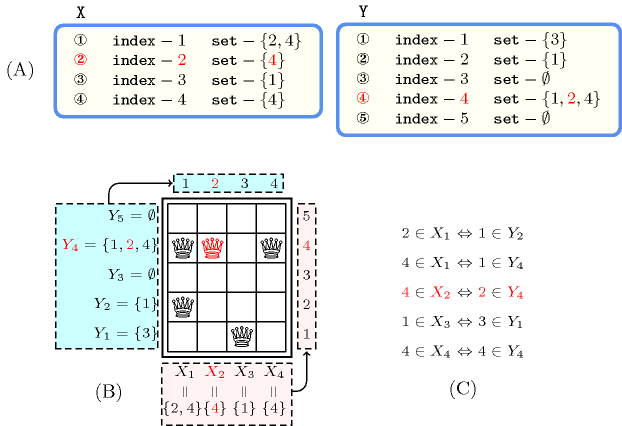
The $𝚒𝚗𝚟𝚎𝚛𝚜𝚎_𝚜𝚎𝚝$ constraint can for instance be used in order to model problems where one has to place items on a rectangular board in such a way that a column or a row can have more than one item. We have one set variable for each row of the board; Its values are the column indexes corresponding to the positions where an item is placed. Similarly we have also one set variable for each column of the board; Its values are the row indexes corresponding to the positions where an item is placed. The $𝚒𝚗𝚟𝚎𝚛𝚜𝚎_𝚜𝚎𝚝$ constraint maintains the link between the rows and the columns variables. Figure 5.201.1 shows the board that can be associated with the example of the Example slot.

Figure 5.201.1. Illustration of the Example slot where we highlight in red the second item of the $𝚇$ collection and the fourth item of the $𝚈$ collection showing the relation between $X_{2}$ and $Y_{4}$ , where $X_{i}$ (with $1 \leq i \leq 4$ ) and $Y_{j}$ (with $1 \leq j \leq 5$ ) respectively stands for the set attribute of the $i^{𝚝𝚑}$ item of the $𝚇$ collection and of the $j^{𝚝𝚑}$ item of the $𝚈$ collection (A) Collections $𝚇$ and $𝚈$ passed to the $𝚒𝚗𝚟𝚎𝚛𝚜𝚎_𝚜𝚎𝚝$ constraint, (B) Corresponding board, (C) Conditions linking the items of $𝚇$ and the items of $𝚈$ .

Systems

inverseSet in Choco, inverse_set in MiniZinc.

specialisation: $𝚒𝚗𝚟𝚎𝚛𝚜𝚎$ ( $𝚜𝚎𝚝$ $𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎$ replaced by $𝚍𝚘𝚖𝚊𝚒𝚗 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎$ ).

used in graph description: $𝚒𝚗_𝚜𝚎𝚝$ .

Keywords

constraint arguments: constraint involving set variables.

modelling: channelling constraint, set channel, dual model.

Arc input(s)

$𝚇$ $𝚈$

Arc generator

𝑃𝑅𝑂𝐷𝑈𝐶𝑇

\mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚡, 𝚢)

Arc arity

Arc constraint(s)

𝚒𝚗_𝚜𝚎𝚝

(𝚢 . 𝚒𝚗𝚍𝚎𝚡, 𝚡 . 𝚜𝚎𝚝) \Leftrightarrow

𝚒𝚗_𝚜𝚎𝚝

(𝚡 . 𝚒𝚗𝚍𝚎𝚡, 𝚢 . 𝚜𝚎𝚝)

Graph property(ies)

𝐍𝐀𝐑𝐂

= | 𝚇 | * | 𝚈 |

Graph model

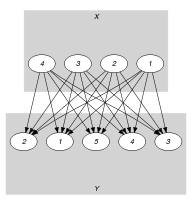
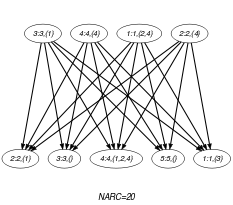
Parts (A) and (B) of Figure 5.201.2 respectively show the initial and final graph associated with the Example slot. Since we use the $𝐍𝐀𝐑𝐂$ graph property, the arcs of the final graph are stressed in bold.

Figure 5.201.2. Initial and final graph of the $𝚒𝚗𝚟𝚎𝚛𝚜𝚎_𝚜𝚎𝚝$ constraint


(a)	(b)

Global Constraint Catalog

5. Global Constraint Catalogue

5.201. inverse_set

Figure 5.201.2. Initial and final graph of the 𝚒𝚗𝚟𝚎𝚛𝚜𝚎_𝚜𝚎𝚝 constraint

Figure 5.201.2. Initial and final graph of the $𝚒𝚗𝚟𝚎𝚛𝚜𝚎_𝚜𝚎𝚝$ constraint