Global Constraint Catalog: Cmax_increasing

5.241. max_increasing_slope

DESCRIPTION

LINKS

AUTOMATON

Origin

Motivated by time series.

Constraint

$𝚖𝚊𝚡_𝚒𝚗𝚌𝚛𝚎𝚊𝚜𝚒𝚗𝚐_𝚜𝚕𝚘𝚙𝚎 (𝙼𝙰𝚇, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

Arguments

$𝙼𝙰𝚇$	$𝚍𝚟𝚊𝚛$
$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)$

Restrictions

𝙼𝙰𝚇 \geq 0

𝙼𝙰𝚇 <

𝚛𝚊𝚗𝚐𝚎

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛)

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚟𝚊𝚛)

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | > 0

Purpose

Given a sequence of variables $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 = V_{1}, V_{2}, \dots, V_{n}$ , sets $𝙼𝙰𝚇$ to 0 if $∄ i \in [1, n - 1] | V_{i} < V_{i + 1}$ , otherwise sets $𝙼𝙰𝚇$ to ${max}_{i \in [1, n - 1] | V_{i} < V_{i + 1}} (V_{i + 1} - V_{i})$ .

Example

(4, 〈1, 1, 5, 8, 6, 2, 2, 1, 2〉)

(0, 〈9, 8, 6, 4, 1, 0〉)

(8, 〈9, 6, 6, 4, 1, 9〉)

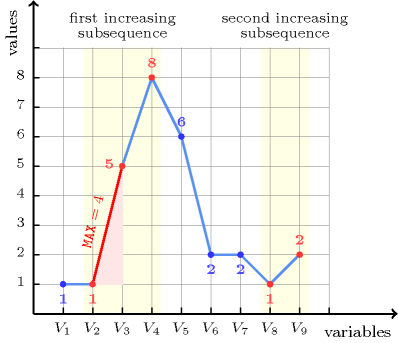
The first $𝚖𝚊𝚡_𝚒𝚗𝚌𝚛𝚎𝚊𝚜𝚒𝚗𝚐_𝚜𝚕𝚘𝚙𝚎$ constraint holds since the sequence $115862212$ contains two increasing subsequences $158$ and $12$ and the maximum slope is equal to $max (5 - 1, 8 - 5, 2 - 1) = 4$ as shown on Figure 5.241.1.

Figure 5.241.1. Illustration of the first example of the Example slot: a sequence of nine variables $V_{1}$ , $V_{2}$ , $V_{3}$ , $V_{4}$ , $V_{5}$ , $V_{6}$ , $V_{7}$ , $V_{8}$ , $V_{9}$ respectively fixed to values 1, 1, 5, 8, 6, 2, 2, 1, 2 and the corresponding maximum slope on the strictly increasing subsequences $158$ and $12$ ( $𝙼𝙰𝚇 = 4$ )

Typical

𝙼𝙰𝚇 > 0

𝙼𝙰𝚇 <

𝚛𝚊𝚗𝚐𝚎

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) - 1

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | > 2

𝚛𝚊𝚗𝚐𝚎

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) > 2

Symmetry

One and the same constant can be added to the $𝚟𝚊𝚛$ attribute of all items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ .

Arg. properties

Functional dependency: $𝙼𝙰𝚇$ determined by $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ .

Usage

Getting the maximum slope over the increasing sequences of time series.

Counting

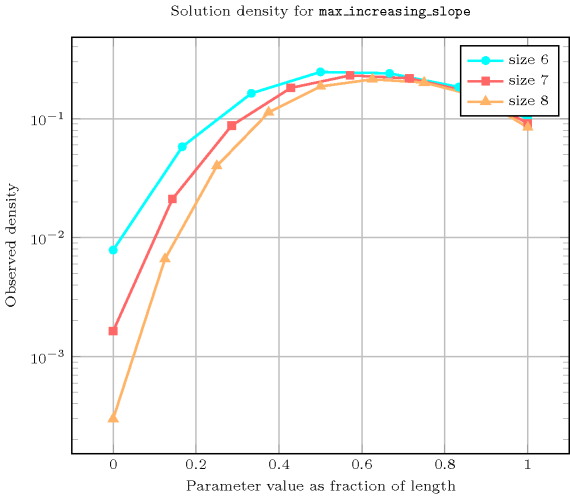
Length ( $n$ )	2	3	4	5	6	7	8
Solutions	9	64	625	7776	117649	2097152	43046721

Number of solutions for $𝚖𝚊𝚡_𝚒𝚗𝚌𝚛𝚎𝚊𝚜𝚒𝚗𝚐_𝚜𝚕𝚘𝚙𝚎$ : domains $0 . . n$

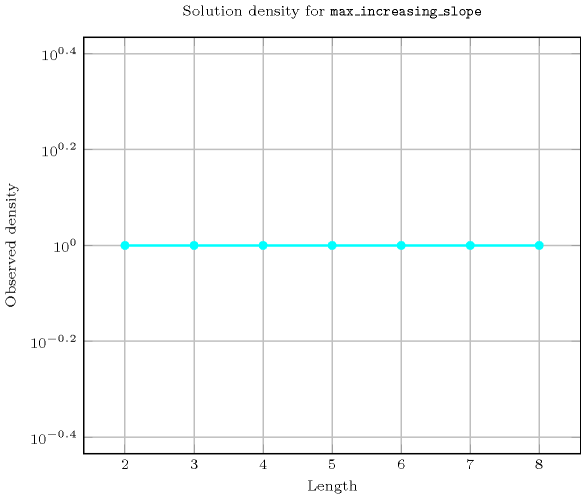
ctrs/max_increasing_slope-2-tikz

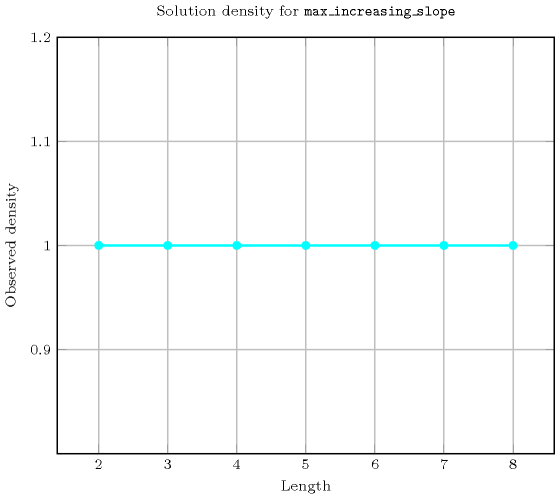
ctrs/max_increasing_slope-3-tikz

Length (

n

)

Total

625

7776

117649

2097152

43046721

Parameter

value

252

924

3432

12870

151

1036

6828

44220

284405

188

1952

19200

183304

1721425

142

2106

29035

380116

4847301

1584

28266

483840

8021350

846

21684

457632

9208124

11712

353088

8654931

191520

6673834

3622481

Solution count for $𝚖𝚊𝚡_𝚒𝚗𝚌𝚛𝚎𝚊𝚜𝚒𝚗𝚐_𝚜𝚕𝚘𝚙𝚎$ : domains $0 . . n$

ctrs/max_increasing_slope-4-tikz

ctrs/max_increasing_slope-5-tikz

Keywords

characteristic of a constraint: automaton, automaton with counters.

combinatorial object: sequence.

constraint arguments: reverse of a constraint, pure functional dependency.

filtering: glue matrix.

modelling: functional dependency.

Cond. implications

$•$ $𝚖𝚊𝚡_𝚒𝚗𝚌𝚛𝚎𝚊𝚜𝚒𝚗𝚐_𝚜𝚕𝚘𝚙𝚎 (𝙼𝙰𝚇, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

with $𝚛𝚊𝚗𝚐𝚎$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) = 𝙼𝙰𝚇 + 1$

implies $𝚕𝚘𝚗𝚐𝚎𝚜𝚝_𝚒𝚗𝚌𝚛𝚎𝚊𝚜𝚒𝚗𝚐_𝚜𝚎𝚚𝚞𝚎𝚗𝚌𝚎$ $(𝙻, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

when $𝚛𝚊𝚗𝚐𝚎$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) = 𝙻 + 1$ .

$•$ $𝚖𝚊𝚡_𝚒𝚗𝚌𝚛𝚎𝚊𝚜𝚒𝚗𝚐_𝚜𝚕𝚘𝚙𝚎 (𝙼𝙰𝚇, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

with $𝙼𝙰𝚇 = 1$

implies $𝚖𝚒𝚗_𝚒𝚗𝚌𝚛𝚎𝚊𝚜𝚒𝚗𝚐_𝚜𝚕𝚘𝚙𝚎$ $(𝙼𝙸𝙽, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

when $𝙼𝙸𝙽 = 1$ .

Automaton: Figure 5.241.2 depicts the automaton associated with the $𝚖𝚊𝚡_𝚒𝚗𝚌𝚛𝚎𝚊𝚜𝚒𝚗𝚐_𝚜𝚕𝚘𝚙𝚎$ constraint. To each pair of consecutive variables $({𝚅𝙰𝚁}_{i}, {𝚅𝙰𝚁}_{i + 1})$ of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ corresponds a signature variable $S_{i}$ . The following signature constraint links ${𝚅𝙰𝚁}_{i}$ , ${𝚅𝙰𝚁}_{i + 1}$ and $S_{i}$ : $({𝚅𝙰𝚁}_{i} \geq {𝚅𝙰𝚁}_{i + 1} \Leftrightarrow S_{i} = 0) \land ({𝚅𝙰𝚁}_{i} < {𝚅𝙰𝚁}_{i + 1} \Leftrightarrow S_{i} = 1)$ .

Figure 5.241.2. Automaton for the $𝚖𝚊𝚡_𝚒𝚗𝚌𝚛𝚎𝚊𝚜𝚒𝚗𝚐_𝚜𝚕𝚘𝚙𝚎$ constraint and its glue matrix (note that the reverse of $𝚖𝚊𝚡_𝚒𝚗𝚌𝚛𝚎𝚊𝚜𝚒𝚗𝚐_𝚜𝚕𝚘𝚙𝚎$ is $𝚖𝚊𝚡_𝚍𝚎𝚌𝚛𝚎𝚊𝚜𝚒𝚗𝚐_𝚜𝚕𝚘𝚙𝚎$ )

Global Constraint Catalog

5. Global Constraint Catalogue

5.241. max_increasing_slope