5.326. precedence
| DESCRIPTION | LINKS | GRAPH |
- Origin
Scheduling
- Constraint
- Argument
- Restrictions
- Purpose
All consecutive pairs of tasks of the collection should be ordered (i.e., the end of the first task of a pair should be less than or equal to the start of the second task of the same pair).
- Example
-
Since the tasks are ordered (i.e., , , ) the constraint holds.
- Typical
- Symmetries
- Arg. properties
Contractible wrt. .
- See also
common keyword: (order constraint).
implies: .
- Keywords
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
- Graph property(ies)
-
- Graph model
Since we are only interested by the constraints linking two consecutive items of the collection we use to generate the arcs of the initial graph.
Parts (A) and (B) of Figure 5.326.1 respectively show the initial and final graph of the first example of the Example slot. Since we use the graph property, the arcs of the final graph are stressed in bold.
Figure 5.326.1. Initial and final graph of the constraint
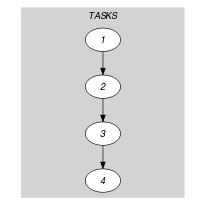
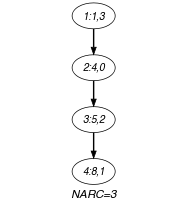
(a) (b)